常用公式：

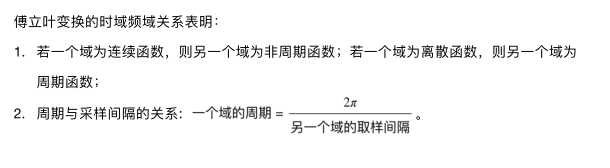
x(n)的z变换为

x(n)的离散时间傅立叶正变换为

的离散傅立叶级数变换为

3.1傅立叶变换的四种形式

3.1.1.连续时间函数的傅立叶变换

时间是连续的，非周期的：■连续时间函数的傅立叶变换/傅立叶变换（CFT/FT）

时间是连续的，周期的：■连续周期信号的傅立叶级数（CFS）

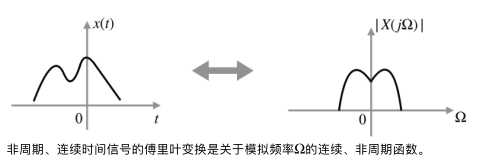
连续时间周期信号可以用一系列谐波分量的线性组合来表征。

展开式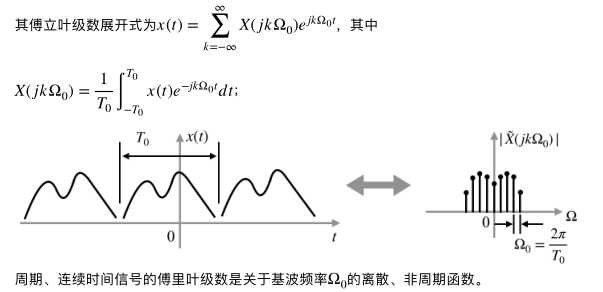：稍后会有总结，别怕分不清

3.1.2.连续时间序列的傅立叶变换

■离散时间傅立叶变换（DTFT）

■离散傅立叶级数（DFS）

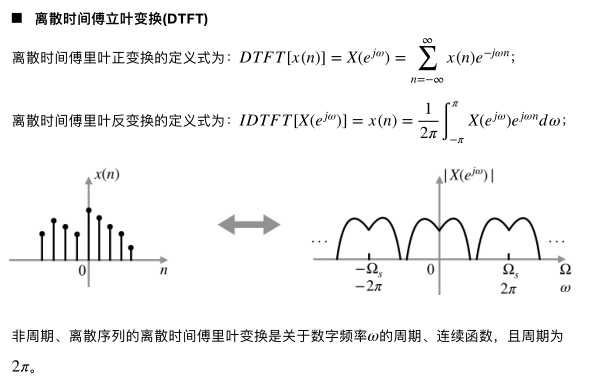
对有限长序列的DTFT进行频域采样，则该序列会在时域中周期延拓；则周期序列对应的频谱是离散且周期的，可以用一系列谐波分量的线性组合表征周期序列；

3.1.3.傅立叶变换的时、频域关系

■傅立叶变换的时、频域关系

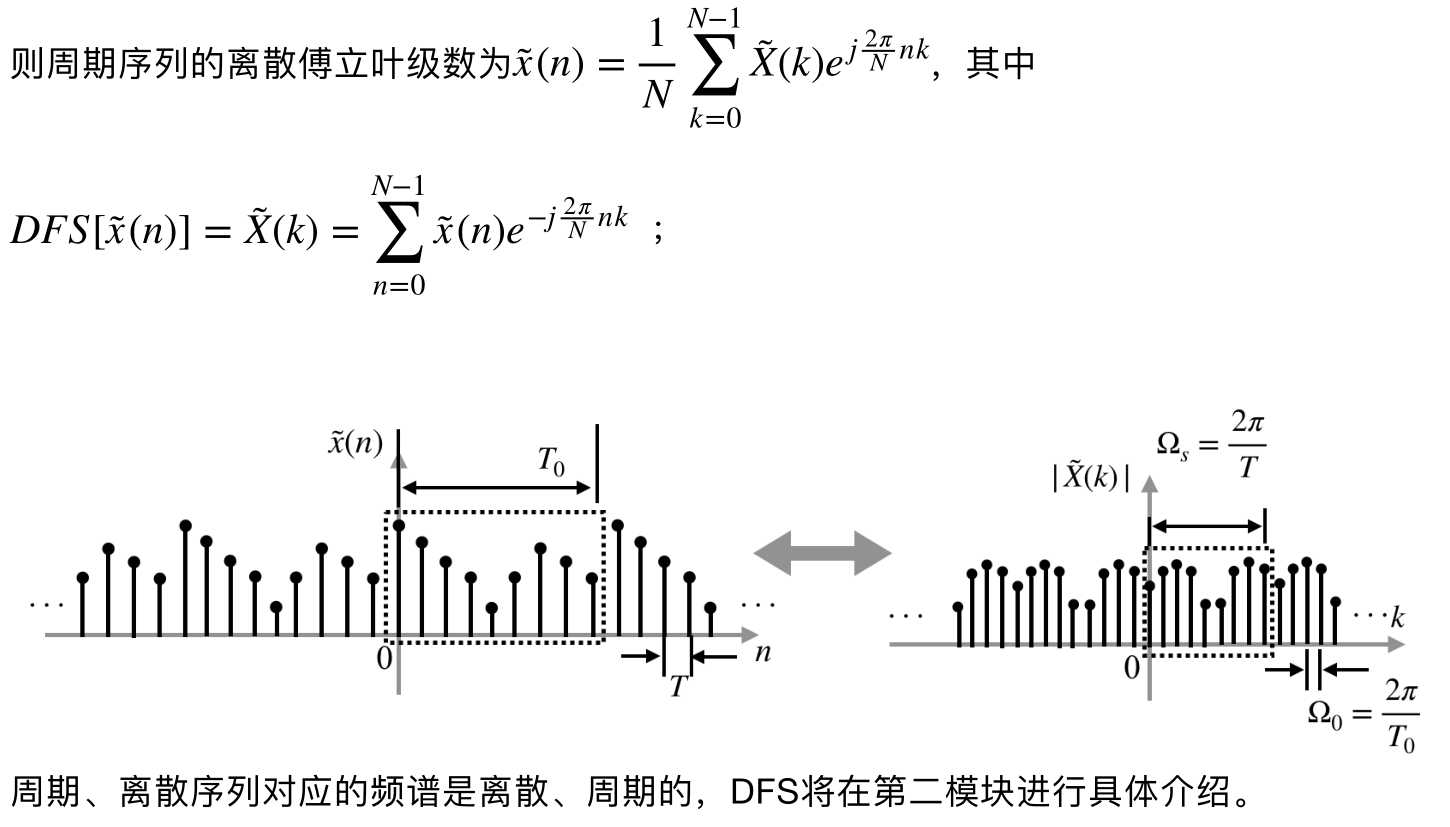
傅里叶变换指的是时间信号和频谱函数之间的变换关系。

巧记：

非连周离   +   时域连续—>频域非周期；时域离散—>频域周期

3.2.周期序列的傅立叶变换DFS

因为是以N为周期延拓的，所以只要做一个周期内的级数变换就可以了

3.2.1.离散傅立叶级数DFS

■离散傅立叶级数（DFS）---定义式

■离散傅立叶级数（DFS）--旋转因子的定义

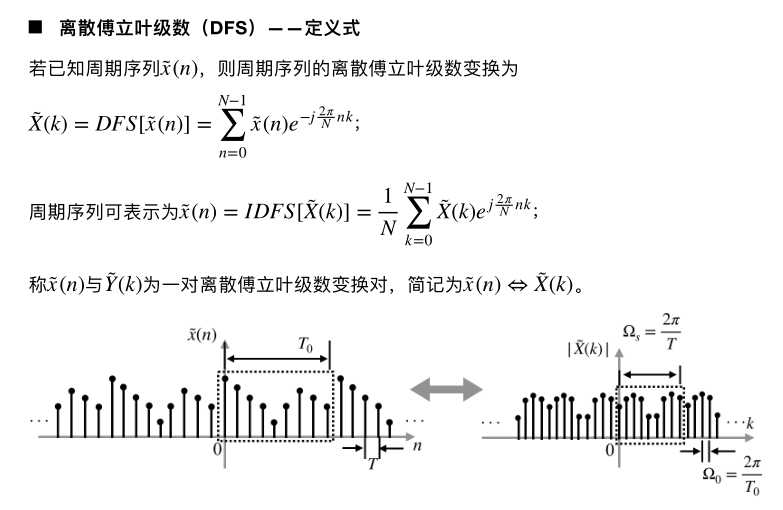
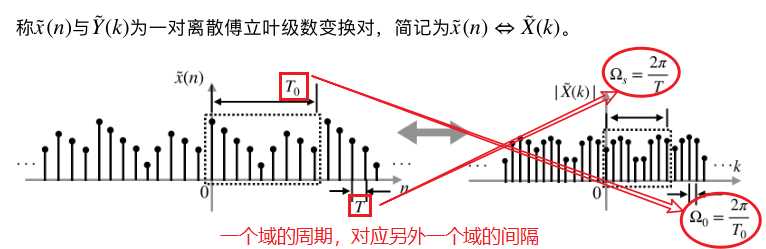
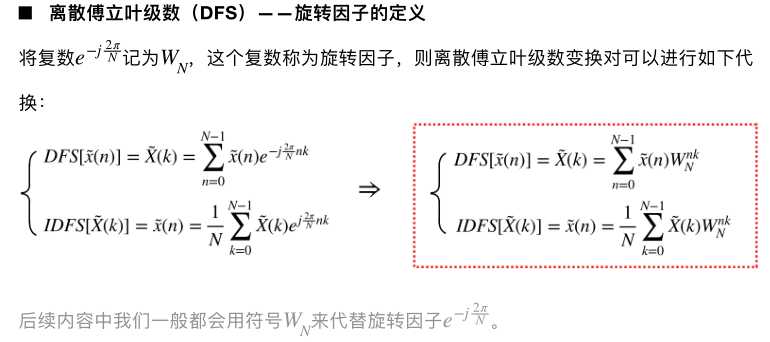
 正对负

■离散傅立叶级数（DFS）--旋转因子的性质

虚字是推导

 ①里面取负，和外面取共轭正好抵消了

②可约性对FFT有帮助，W上面的i可以往下移动

③旋转因子有周期性

⑤e的jΠ=1，e的-jΠ=-1

3.2.2.变换间的关系

■DFS与z变换、DTFT的关系

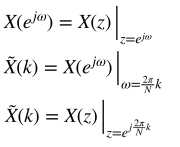
②DFS对DTFT在2Π周期内做了一个N点的采样

③Z变换在单位圆上做变换，就是DTFT

DTFT在做一个等间隔采样，得到DFS

——>在单位圆做一个等间隔采样就能得到DFS

做一个周期序列N=8的例子

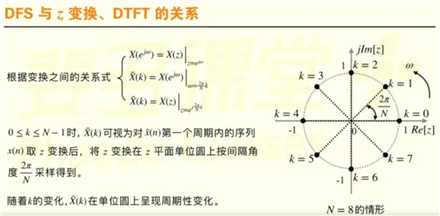
 在单位圆做一个8点的等间隔采样就能得到DFSx~

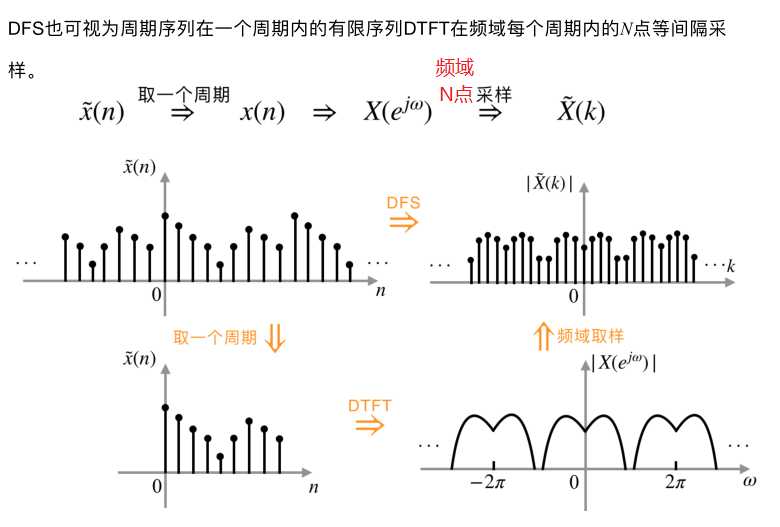
等比数列求和公式：，

sinx=[e^(ix)-e^(-ix)]/(2i)，cosx=[e^(ix)+e^(-ix)]/2 ，又用到了欧拉公式

 3.2.3.DFS的性质

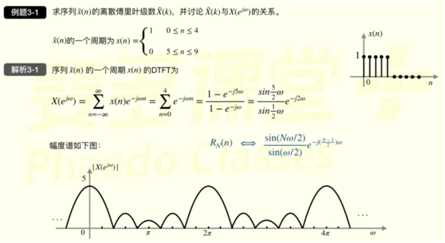
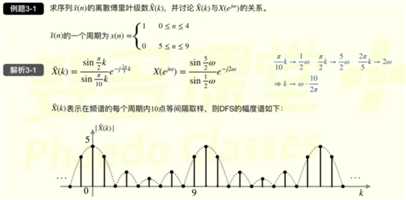
DFS是周期离散序列的傅立叶变换，因此DFS具有一些可以类比CFT的性质。

■DFS 的性质--线性性质

 注意必须要周期相等，才能线性组合

 ■DFS 的性质--移位性质

 注意符号的正负

 后面不写了，来不及复习了，刷原题去

【数字信号处理不挂科-笔记】第三讲-离散傅立叶变换

原文：https://www.cnblogs.com/guoxinyu/p/buguake-szxhcl2.html