图论
图论,说白了就是一个图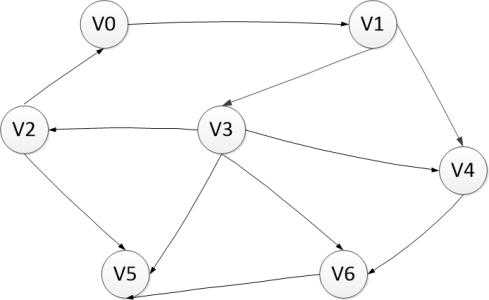
图论,并不是让你用Python的turtle画一个。简单来说,如果我们伟大的先人没有发明图论这个东西的话,就没有今天的地图导航、外卖、飞机等等很多东西都是幻想。
图论,主要是研究它的最短路径。就拿上图来说↑,这个图是一个有向无权图。如果有一个小人,他想从v1坐公交车做到v5,但他会晕车,所以你需要求出从v1走到v5的最短路径,以免他晕车。
那么,如何让计算机这个笨蛋全自动化一下,自己求出从v1到v5的最短路径呢?这就需要一些最短路算法算法来解决了,比如说:Dijkstra、Bellman-Ford等等都是用来计算最短路径的算法。
下面是一组数据:
5 //一共有5条路与5个点 1 3 2 //表示从点1到点3有一条权值(长度)为2的路 2 5 1 1 2 1 4 5 4 2 3 5 //无向图
当我们高高兴兴地准备开打代码时,我们又会发现一个问题:怎么将输入的图存储到计算机中呢?
这就需要一个很“强大”的存储方法:邻接矩阵!!!
我们先来看数据,节点1到节点3之间有一条路,权值(长度)为5,我们可以将这一条路存到一个二维数组里:
int graph[NUM][NUM]; int a,b,c; scanf("%d",&a,&b,&c);//a,b为这条边的两个端点,c为这条边的权值(长度)。 graph[a][b]=c;
graph数组表示的是第i个节点到第j个节点的长度为graph[i][j]。
注意:如果graph[i][j]=INF,则表示节点i到节点j无边。
邻接矩阵可是个好东西,因为代码非常好打,所以打代码的速度就比较快。而且,看完代码我们也可以发现,它对边的储存、查询、更新等操作又快又简单,只要进一步就能访问和修改。
但他也有一些缺点:他的储存复杂度(O(V^2))太高了 ,如果用来储存稀疏图,那么空间将大大被浪费。当V=10 000个节点时,graph的空间为100MB,这已经超出了常见图论的题了,所以,我们伟大的先人又发明了一个东西叫做:邻接表!!!(今天先不说)
最后,附上一道基础题:hdu 2544(acm.hdu.edu.cn)
(邻接矩阵模板代码:)
#include <bits/stdc++.h> using namespace std; const int INF=0x3f; int graph[10000][10000]; void Adjacency_Matrix(int a,int b,int c) { graph[a][b]=c;//邻接矩阵的精髓 } int main( ) { int n; scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) graph[i][j]=INF;//预处理,每个都赋值为INF for(int i=1;i<=n;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c);//输入每条边的端点以及权值 Adjacency_Matrix(a,b,c);//邻接矩阵存图 } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(graph[i][j]!=INF)//如果graph[i][j]为INF,则说明当前i,j之间没有边 printf("%d %d %d\n",i,j,graph[i][j]);//为了表明邻接矩阵的存图功能,从边的端点编号依次输出另一个端点以及其权值 else continue; } } return 0; }
下次,本博主还会和大家聊一聊一个更强的存图方式:邻接表!!!
原文:https://www.cnblogs.com/8-26-3/p/12082937.html