前缀和与差分

本篇博客适合初学者阅读，如有不周之处，欢迎各位大佬指正！

• 0.背景

想象一下，你有一个数组（ ****很长很长de那种**** ）你需要求出给定一段区间的和，并有多次询问，作为初学者你是否要\(\boxed{for}\)循环把他们都加起来呢？

• 1.正文

前缀和

前缀和是一个数列A通过递推能够求出来的信息之一，顾名思义就是某个数前面所有单元数值之和。他的公式如下
\[S_i=\sum\limits_{j=1}^iA_j\]

对于给定数列A，我们可以通过如下代码实现前缀和

for(rg int i=1;i<=n;i++){
    S[i]=S[i-1]+A[i]
}

代码中的 \(S[i]=S[i-1]+A[i]\) 就是前缀和的递推式

一个问题：如果我们想要求一个区间$ [l,r]$的和，我们应该如何实现？

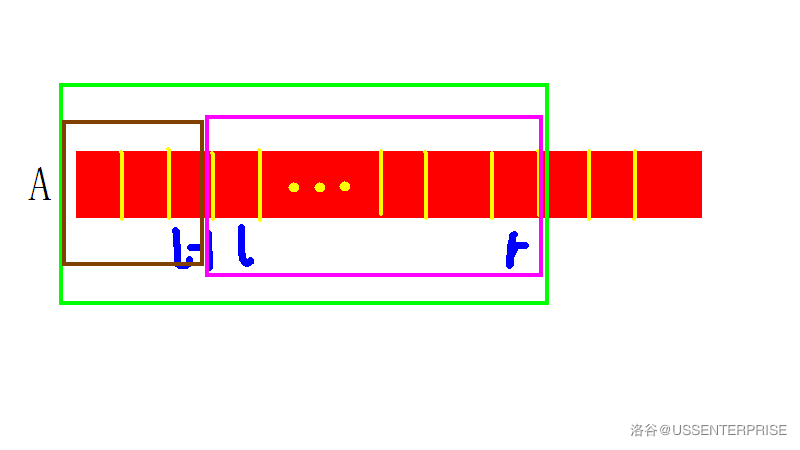
由于\(S\)代表数列\(A\)的前缀和，我们想要求一个闭区间的和只需要去掉\(l\)之前的所有部分就行了
\[ ans=\sum\limits_{i=l}^rA_i=S_r-s_{l-1} \]

所以我们就求出了\([l,r]\)的和

差分

对于一个给定数列\(A\)，它的差分数列\(C\)定义为
\[B_i=A_i-A_{i-1}\text{ } (2\leq i\leq n)\]
差分可以看做前缀和的逆运算

你可以认为\(\boxed{\text{前缀和数列}}\)的\(\boxed{\text{差分数列}}\)就是\(\boxed{\text{原数列}}\)，\(\boxed{\text{差分数列}}\)的\(\boxed{\text{前缀和数列}}\)也是\(\boxed{\text{原数列}}\)

利用差分，我们可以区间多次以\(O(1)\)复杂度区间修改一个数组

实现方法：

我们将原数组想象为高度不同的一片高楼(如下图)

//未完待续

【算法学习笔记】前缀和与差分

原文：https://www.cnblogs.com/UssEnterprise/p/12085229.html