题目链接:http://acm.csust.edu.cn/problem/3022
Description
世界杯足球赛的最后一个阶段是用附加赛制度进行的。
这一阶段还剩n支队伍,从1到n进行计数。
进行几轮,在每轮中,剩余的队伍按其ID的顺序进行排序,
然后按此顺序第一支队伍与第二支队伍、第三支队伍与第四支队伍、第五支队伍与第六支队伍进行比赛,依此类推。
保证每一轮都有偶数支队伍。每场比赛的赢家晋级下一轮,输家被淘汰出局,没有平局。
在最后一轮比赛中,只有剩下两支队伍:这一轮称为决赛,胜者称为冠军,比赛结束。
jcc想让他最喜欢的两支球队参加决赛。
不幸的是,球队的身份已经确定,可能会发生球队不可能在决赛中相遇的情况,不过jcc非常有钱,
可以通过花钱来决定任意两只队伍的胜负,所以确保了a,b一定会在某场比赛相遇,但由于赛制问题,不能保证在决赛相遇,但会保证他们能相遇。
求具有a和b两只队伍在多少轮之后可以相遇,若能在决赛相遇,则输出“Final!”,否则输出在多少轮之后可以相遇。
Input
唯一一行包含三个整数n,a和b(2 ≤ n ≤256,1 ≤ a,b ≤ n)-代表团队总数,以及jcc感兴趣的团队的ID。(a!=b)
Output
如果a队和b队能在决赛中相遇,在唯一的一行中打印“Final!”。
否则,请打印一个整数,表示a和b在多少轮之后可以相遇。
Sample Input 1
4 1 2
Sample Output 1
1
Sample Input 2
8 2 6
Sample Output 2
Final!
由于每轮都是偶数只队伍,那么这就相当于一颗满二叉树了,我们经常看电视的时候每次比赛都基本会出现树状图。
我们每次只记录叶节点的编号(假设为i),那么下一次的新叶节点编号(即旧叶节点的父亲)为(i+1)/2如图所示:
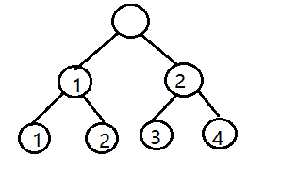
那么他们相遇也就是父节点相同的时候,而每找一次父节点计数器加一,则最后的计数器的值(记为S)就是树的深度-1,也是比赛是场数,最后如果2S为总的队伍数,则说明决赛相遇。
以下是AC代码:
#include <bits/stdc++.h> using namespace std; int pow(int a,int s) { int ans=1; for (int i=1; i<=s; i++) ans*=a; return ans; } int main() { int n,a,b; scanf ("%d%d%d",&n,&a,&b); int s=0; while (a!=b){ a=(a+1)/2; b=(b+1)/2; s++; } if (n-pow(2,s)==0) printf ("Final!\n"); else printf ("%d\n",s); return 0; }
原文:https://www.cnblogs.com/lonely-wind-/p/12003934.html