数据分析 numpy数组_06 字节交换，副本和视图、NumPy 矩阵库(Matrix)、NumPy IO 、

NumPy 字节交换

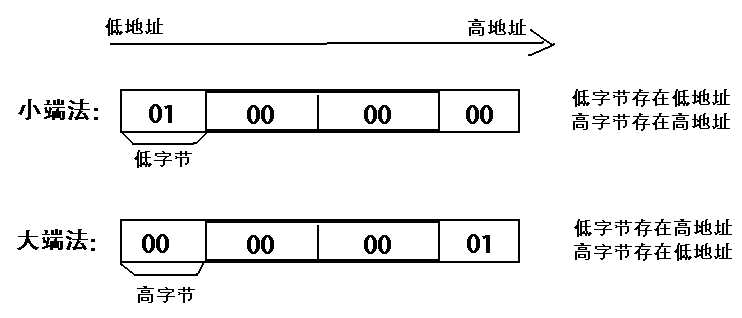
　　大端模式：指数据的高字节保存在内存的低地址中，而数据的低字节保存在内存的高地址中，这样的存储模式有点儿类似于把数据当作字符串顺序处理：地址由小向大增加，而数据从高位往低位放。

　　小端模式：指数据的高字节保存在内存的高地址中，而数据的低字节保存在内存的低地址中，这种存储模式将地址的高低和数据位权有效地结合起来，高地址部分权值高，低地址部分权值低。

　　numpy.ndarray.byteswap() 函数将 ndarray 中每个元素中的字节进行大小端转换。

NumPy 副本和视图

　　副本是一个数据的完整的拷贝，如果我们对副本进行修改，它不会影响到原始数据，物理内存不在同一位置。

　　视图是数据的一个别称或引用，通过该别称或引用亦便可访问、操作原有数据，但原有数据不会产生拷贝。如果我们对视图进行修改，它会影响到原始数据，物理内存在同一位置???

视图一般发生在：

• 1、numpy 的切片操作a[...:2],使用切片创建视图修改数据会影响到原始数组,但是切片的id和原始数组的id是不一样的;numpy数组操作中的numpy.ravel()，
• 2、调用 ndarray 的 view() 函数产生一个视图:numpy.ndarray.view()。该方法创建的新数组的维数更改不会更改原始数据的维数。不是前后矛盾了吗？

副本一般发生在：

• Python 序列的切片操作，调用deepCopy()函数。
• 调用 ndarray 的 copy() 函数产生一个副本，对副本数据进行修改，不会影响到原始数据，它们物理内存不在同一位置。

赋值　　

　　a = b，访问a是使用原始数组b的相同id()来访问,b数组的任何变化都反映在a数组上。

NumPy 矩阵库(Matrix)

　　import numpy.matlib中的函数；matlib.empty()、numpy.matlib.zeros()、numpy.matlib.ones()、

　　numpy.matlib.eye(n, M,k, dtype)返回一个矩阵，对角线元素为 1，其他位置为零。

　　numpy.matlib.identity(5, dtype = float)，给定大小的单位矩阵，单位矩阵是个方阵

　　numpy.matlib.rand(3, 3) 函数创建一个给定大小的矩阵，数据是随机填充的　　

实例讲解numpy.matlib.eye()中的属性 k

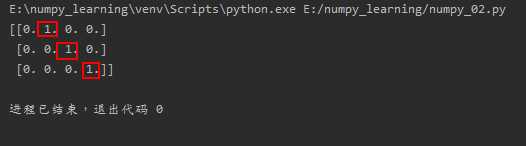
import numpy.matlib
import numpy as np

print(np.matlib.eye(n=3, M=4, k=1, dtype=float))

NumPy 线性代数

NumPy 提供了线性代数函数库 linalg。

笔记：

　　1、numpy.matmul 函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积，但如果任一参数的维数大于2，参数为N维，该参数是一些矩阵(最后两个维数为矩阵维数)的stack，也就是进行矩阵运算运算，并进行相应广播(四维是怎么样的？？？？？)。另一方面，如果任一参数是一维数组，则通过在其维度上附加 1 来将其提升为矩阵，并在乘法之后被去除。对于二维数组，它就是矩阵乘法。

　　2、NumPy 中对 array 使用 multiply() 或 * 操作符并不是矩阵乘法，两个是‘element-wise’，正确的用法是 dot() 或 matmul()，或者对 matrix 使用 *

　　3、nxn维矩阵的行列式怎么求？怎么由定义的余子式，代数余子式，利用定义任意一行(列)中的每一个元素和其代数余子式的乘积的和就是nxn维矩阵的行列式推出其他计算方法的来源呢？？？

NumPy IO 

常用的 IO 函数有：

• load() 和 save(file, arr, allow_pickle=True, fix_imports=True) 函数是读写文件数组数据的两个主要函数，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。
• savze(file, *args, **kwds) 函数用于将多个数组写入文件，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。
• loadtxt(FILENAME, dtype=int, delimiter=‘ ‘) 和 savetxt(FILENAME, a, fmt="%d", delimiter=",") 函数处理正常的文本文件(.txt 等)

数据分析 numpy数组_06 字节交换，副本和视图、NumPy 矩阵库(Matrix)、NumPy IO 、

原文：https://www.cnblogs.com/yinminbo/p/11442619.html