学号 20182329 2019-2020-1 《数据结构与面向对象程序设计》实验9报告

• 课程：《程序设计与数据结构》
• 班级： 1823
• 姓名： 李一卓
• 学号：20182329
• 实验教师：王志强
• 实验日期：2019年12月3日
• 必修/选修： 必修

1.实验内容

• 实现二叉排序树，并学会编写删除、添加、插入，还有二叉排序树的遍历
• 学习图的有关知识，了解有向图和无向图的区别，
• 学习带权图，学会计算带权图的算法，最佳的算法。
• 学习图的各种遍历，比如深度优先遍历和广度优先遍历。
• 学习生成最小树的方法
• 学会生成图的邻接矩阵的方法，还有计算每个节点的出度入度方法实现
• 学会每个图的计算度的方法，还有不通过遍历进行的。
• 完成有向图的单源最短路径求解（迪杰斯特拉算法）。

2. 实验过程及结果

• 初始化：根据屏幕提示，初始化无向图和有向图（可用邻接矩阵，也可用邻接表），图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输入顶点和边数），我首先根据自己的邻接矩阵实现图。

初始化：

 public Graph(List<Vertex> vertexs, int[][] edges) {
            this.vertexs = vertexs;
            this.topVertexs=new ArrayList<GRAPGAPI.Vertex>();
            this.edges = edges;
            this.minTree=new int[this.vertexs.size()][this.vertexs.size()];
            initUnVisited();
        }

首先得初始化图，获得定点代码

public List<Vertex> getNeighbors(Vertex v) {
            //参数检测
            if(!isInGraph(v)){
                System.out.println("当前节点不在图中");
                return null;
            }
            List<Vertex> neighbors = new ArrayList<Vertex>();
            int position = vertexs.indexOf(v);
            Vertex neighbor = null;
            int distance;
            for (int i = 0; i < vertexs.size(); i++) {
                if (i == position) {
                    //顶点本身，跳过
                    continue;
                }
                distance = edges[position][i];    //到所有顶点的距离
                if (distance < Integer.MAX_VALUE) {
                    //是邻居(有路径可达)
                    neighbor = getVertex(i);
                    if (!neighbor.isMarked()) {
                        //如果邻居没有访问过，则加入list;
                        neighbors.add(neighbor);
                    }
                }
            }
            return neighbors;
        }

• 完成有向图和无向图的遍历（深度和广度优先遍历），无向图与有向图相同。

//深度优先
 public void  DFS(String vertexName){
            int id=getIdOfVertexName(vertexName);
            if(id==-1)return;
            vertexs.get(id).setMarked(true);
            System.out.println("遍历到"+vertexs.get(id).getName());
            List<Vertex> neighbors = getNeighbors(vertexs.get(id));
            for(int i=0;i<neighbors.size();i++){
                if(!neighbors.get(i).isMarked()){
                    DFS(neighbors.get(i).getName());
                }
            }
        }

//广度优先
public void BFS(String vertexName){
            int startID=getIdOfVertexName(vertexName);
            if(startID==-1) return;
            List<Vertex> q=new ArrayList<Vertex>();
            q.add(vertexs.get(startID));
            vertexs.get(startID).setMarked(true);
            while(!q.isEmpty()){
                Vertex curVertex=q.get(0);
                q.remove(0);
                System.out.println("遍历到"+curVertex.getName());
                List<Vertex> neighbors = getNeighbors(curVertex);
                for(int i=0;i<neighbors.size();i++){
                    if(!neighbors.get(i).isMarked()){
                        neighbors.get(i).setMarked(true);
                        q.add(neighbors.get(i));
                    }
                }

            }

        }

• 首先进行拓扑排序的时候，无向图是不能进行的，只有有向图可以进行。用邻接矩阵进行拓扑，MAX_VALUE表0.

public void topSort(){
            int[][] tmpEdges=edges;
            int IDofNullPreVertex=getNullPreVertexID(tmpEdges);//获得当前图中无前驱的节点
            while(IDofNullPreVertex!=-1){
                vertexs.get(IDofNullPreVertex).setMarked(true);
                topVertexs.add(vertexs.get(IDofNullPreVertex));//拓扑序列增加
                //边销毁
                for(int j=0;j<this.vertexs.size();j++){
                    if(tmpEdges[IDofNullPreVertex][j]!=Integer.MAX_VALUE){
                        tmpEdges[IDofNullPreVertex][j]=Integer.MAX_VALUE;
                    }
                }
                IDofNullPreVertex=getNullPreVertexID(tmpEdges);
            }

        }

• 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出
  而且可以进行无向图的最小生成树的更新。

public int[][] getMinTree(){
            initMinTree();//初始化最小生成树
            while(!allVisited()){
                Vertex vertex = vertexs.get(getNotMarkedMinVertex());//设置处理节点
                System.out.println("处理：节点"+vertex.getName());
                //顶点已经计算出最短路径，设置为"已访问"
                vertex.setMarked(true);
                //获取所有"未访问"的邻居
                List<Vertex> neighbors = getNeighbors(vertex);
                System.out.println("邻居个数为："+neighbors.size());
                //更新最小生成树
                updateMinEdge(vertex, neighbors);
            }
            System.out.println("search over");
            setMinTree();

            return minTree;
        }

根据图的变化可以进行最小生成树的更新

 public void  updateMinEdge(Vertex vertex, List<Vertex> neighbors){
            //参数检测
            if(!isInGraph(vertex)){
                System.out.println("当前节点不在图中");
                return ;
            }

            for(Vertex neighbor: neighbors){
                int distance = edges[getIdOfVertexName(neighbor.getName())][getIdOfVertexName(vertex.getName())];
                if(neighbor.getAnotherIDinminEdge()==-1){
                    neighbor.setAnotherIDinminEdge(getIdOfVertexName(vertex.getName()));
                    System.out.println(neighbor.getName()+" setEdge To"+vertex.getName()+edges[neighbor.getAnotherIDinminEdge()][getIdOfVertexName(neighbor.getName())]);
                }
                else if(distance <  edges[getIdOfVertexName(neighbor.getName())][neighbor.getAnotherIDinminEdge()]){
                    neighbor.setAnotherIDinminEdge(getIdOfVertexName(vertex.getName()));
                    System.out.println(neighbor.getName()+" setEdge To"+vertex.getName()+edges[neighbor.getAnotherIDinminEdge()][getIdOfVertexName(neighbor.getName())]);
                }
            }
        }

• 最后进行最短路径的生成

首先进行寻找定点的最短路径

public void search(){
            while(!unVisited.isEmpty()){
                Vertex vertex = unVisited.element();
                //顶点已经计算出最短路径，设置为"已访问"
                vertex.setMarked(true);
                List<Vertex> neighbors = getNeighbors(vertex);
                //更新邻居的最短路径
                updatesDistance(vertex, neighbors);
                pop();
            }
            System.out.println("最短路径");
        }

然后根据邻居最短路径的更新，进行的输出

 public List<Vertex> getNeighbors(Vertex v) {
            //参数检测
            if(!isInGraph(v)){
                System.out.println("当前节点不在图中");
                return null;
            }
            List<Vertex> neighbors = new ArrayList<Vertex>();
            int position = vertexs.indexOf(v);
            Vertex neighbor = null;
            int distance;
            for (int i = 0; i < vertexs.size(); i++) {
                if (i == position) {
                    //顶点本身，跳过
                    continue;
                }
                distance = edges[position][i];    //到所有顶点的距离
                if (distance < Integer.MAX_VALUE) {
                    //是邻居(有路径可达)
                    neighbor = getVertex(i);
                    if (!neighbor.isMarked()) {
                        //如果邻居没有访问过，则加入list;
                        neighbors.add(neighbor);
                    }
                }
            }
            return neighbors;
        }

3. 实验过程中遇到的问题和解决过程

• 问题1：在进行生成图的时候，我选择以文件读写的方式写入图的数据
  

• 问题1解决方法：是我在任务读写的方式有问题，我是双循环来进行文件输入图，，用行和“，”隔开，但是在输入“0”时，没有设置内循环的输出条件，所以在每一行走到“0”时就会无限循环。

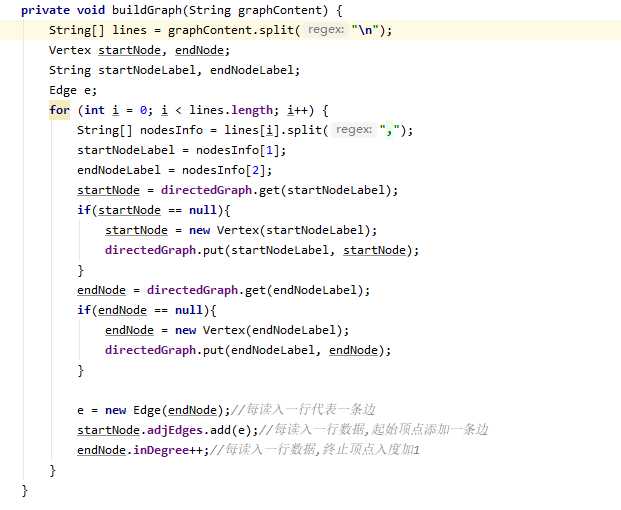
• 问题2：在进行输入图时，进行对节点的最短路径的处理，返现我卡在了第一个节点。
  

• 问题2解决方法：邻接矩阵的输入方式存在敕位问题。

其他（感悟、思考等）

在进行运算生成图的时候，选择链表进行图的生成时，后续的排序会比较麻烦，而且在进行图的顶点的各种操作时（读取），顶点的入度出度会显示。关键在进行各种排序时，还是，还有需要报错程序，这样找不到顶点可以自动返回。

参考资料

• 《Java程序设计与数据结构教程（第二版）》

• 《Java程序设计与数据结构教程（第二版）》学习指导

《数据结构与面向对象程序设计》实验9报告

原文：https://www.cnblogs.com/lyz182329/p/11994388.html