对泛化误差进行分解:
$Err(x)$$=E[(y-f(x;D))^{2}]$
$=E_{D}[f(x;D)-\bar{f}+\bar{f}-y_{D}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}] +E_{D}[(\bar{f}-y_{D})^{2}]+E_{D}[2(f(x;D)-\bar{f})(\bar{f}-y_{D})]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y_{D})^{2}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y+y-y_{D})^{2}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y)^{2}]+E_{D}[(y-y_{D})^{2}]+2E_{D}[(\bar{f}-y)(y-y_{D})]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+(\bar{f}-y)^{2}+E_{D}[(y-y_{D})^{2}]$
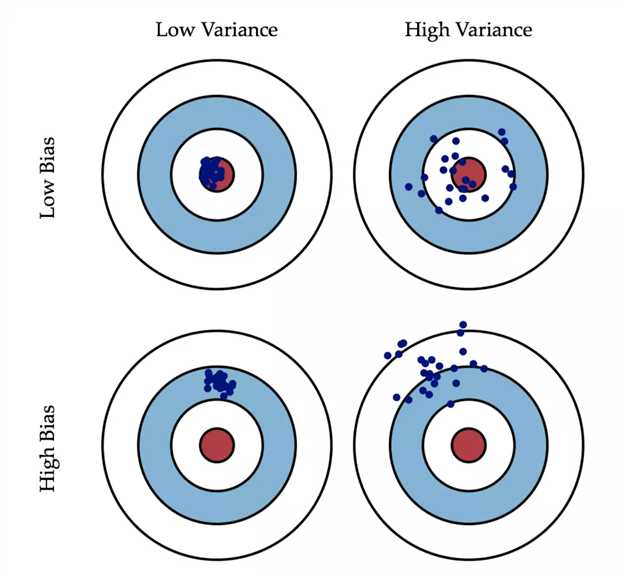
| 测试集误差 | 训练集误差 | 方差 variace | 偏差 bias |
| 小 | 小 | 小 | 小 |
| 大 | 小 | 小(这种情况是过拟合) | 大 |
| 大 | 大 | 大 | 大 |
所以实际情况,我们的方差和偏差都越小越好。
原文:https://www.cnblogs.com/ylxn/p/11972391.html