20182332 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结

教材学习内容总结

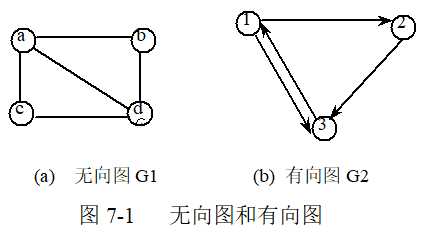
• 在无向图中，表示边的顶点对是无序的。
• 如果图中的两个顶点之间有边连接，则称他们是邻接的；
• 如果无向图中连接顶点的边数达到最大，则图为完全图；
• 路径是图中连接两个顶点的边的序列。
• 图
  • 有向图：一个有向图D是指一个有序三元组(V(D)，A(D)，ψD)，其中ψD为关联函数，它使A(D)中的每一个元素(称为有向边或弧)对应于V(D)中的一个有序元素(称为顶点或点)对。
• 邻接矩阵和关联矩阵定义：设D（V,E）是有向图，其中V={v1,v2,v2…vn},E={e1,e2,e3,…em}称A(D)=(aij)nxn是D的领接矩阵，其中aij是以vi为起始点，以vj为终点的边的条数。
• 度/出度/入度：
  • 在图中，一个顶点依附的边或弧的数目，称为该顶点的度。
  • 在有向图中，一个顶点依附的弧头数目，称为该顶点的入度。
  • 一个顶点依附的弧尾数目，称为该顶点的出度，某个顶点的入度和出度之和称为该顶点的度。
  • 若图中有n个顶点，e条边或弧，第i个顶点的度为di，则有 e=1/2 * Σ(1<= i <= n, di)
• 完全图/稠密图/稀疏图：
  • 具有n个顶点，n(n-1)/2条边的图，称为完全无向图，
  • 具有n个顶点，n(n-1) 条弧的有向图,称为完全有向图。
  • 完全无向图和完全有向图都称为完全图。
  • 对于一般无向图，顶点数为n，边数为e，则 0≤e ≤n(n-1)/2。
  • 对于一般有向图，顶点数为n，弧数为e， 则 0≤e≤n(n-1) 。
  • 当一个图接近完全图时，则称它为稠密图，
  • 当一个图中含有较少的边或弧时，则称它为稀疏图。

• 有向图&无向图：
  

• 权：
  • 在图的边或弧中给出相关的数，称为权。
  • 权可以代表一个顶点到另一个顶点的距离，耗费
    等，带权图一般称为网。

教材学习中的问题和解决过程：

• 图和树有什么区别？
  • 图表
    • 1、图表中每个节点可以有任意数量的边，边可以是单向和双向的。
    • 2、图表中没有名为root的根节点的概念。
    • 3、图表可以有循环和自循环
    • 4、图表中，没有预定义数量的边，它取决于图表。
    • 5、图是网络模型结构。
  • 树
    • 1、常规树由具有任意数量子节点的节点组成；但是在二叉树的情况下，每个节点最多可以有两个子节点。在任意两个节点之间仅存在一条边。
    • 2、树中有一个名为root的唯一节点。
    • 3、树不能有循环和自循环
    • 4、树可以有n-1条边。
    • 5、树是分层结构。

代码调试中的问题和解决过程

• 无法求出权值：

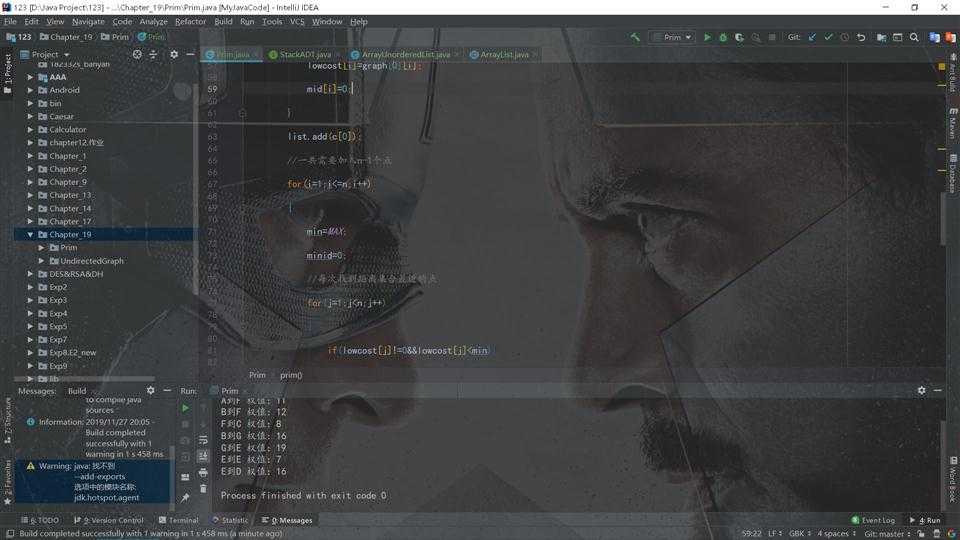
• 解决方案：经过检查后发现是控制寻找距离集合最近的点循环次数有问题

更改为：

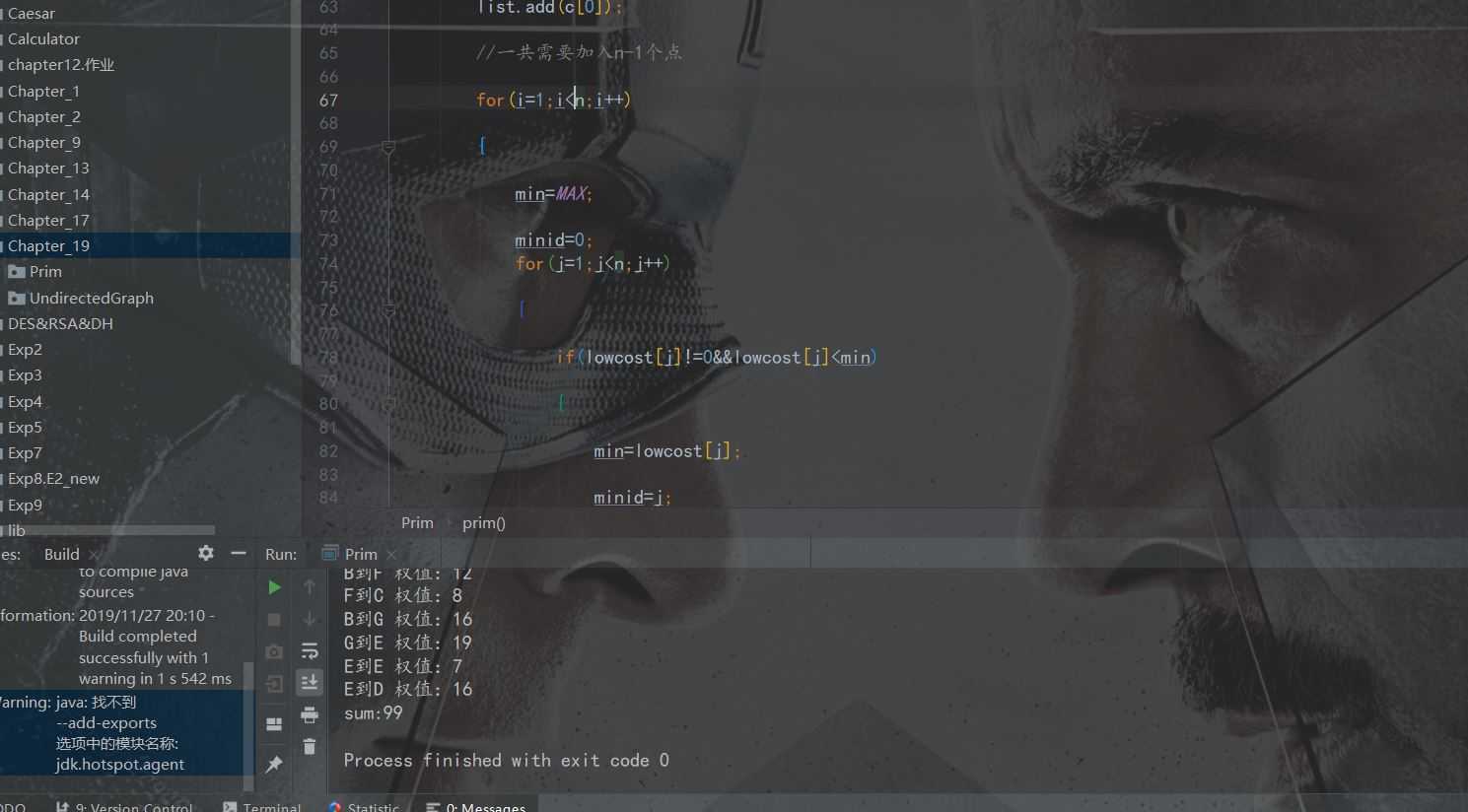
即可

代码托管

上周考试错题总结

上周無考试。

反思：

几个画图的小测试做的还行，但不注重细节，需要多加注意

结对及互评

点评

• 博客中值得学习的：
  • 教材学习内容概括行强，简介明了。
  • 有自己动手打新代码，加入了很多个人的理解。
  • 内容很充实，很用心，比上次进步了很多。
  • 博客格式正确，运用了很多不同的方法，排版精美。

  • 希望能在课本内容总结以及问题&解决过程中加入自己的思考，使博客内容更加充实。
    基于评分标准，我给本博客打分12分：
    得分情况如下：
    正确使用Markdown语法（加1分）
    模板中的要素齐全（加1分）
    教材学习中的问题和解决过程（加2分）
    代码调试中的问题和解决过程（加2分）
    其他加分（加6分）
    进度条中记录学习时间与改进情况（1）
    感想，体会不假大空（1）
    有动手写新代码（1）
    错题学习深入（1）
    点评认真，能指出博客和代码中的问题（1）
    结对学习情况真实可信（1）

    点评过的同学博客和代码

• 本周结对学习情况：
  • [20182316]

其他（感悟、思考等，可选）

思维逐渐离散

参考资料

• 《Java程序设计与数据结构教程（第二版）》

• 《Java程序设计与数据结构教程（第二版）》学习指导

20182332 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结

原文：https://www.cnblogs.com/Stark-GR/p/11945249.html