Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

标签： 入门讲座题解 数论

题目描述

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

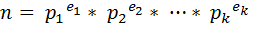
Then we can write,

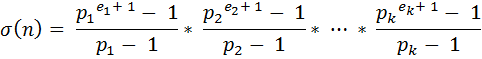
For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 1012).

Output

For each case, print the case number and the result.

Sample Input

4

3

10

100

1000

Sample Output

Case 1: 1

Case 2: 5

Case 3: 83

Case 4: 947

题意

约数和函数\[\sigma{(n)} = \sum_{d | n} d\;.\]
给定\(n\)，询问\([1, n]\)区间内有几个\(i\)，使得\(\sigma{(i)}\)为偶数？

解析

根据算数基本定理，正整数\(n\)，有唯一质因数分解形式，\[n = p_1^{\alpha_1}\cdot p_2^{\alpha_2} \cdot p_3^{\alpha_3} \cdot \,\,\cdots \,\, \cdot p_n^{\alpha_n}\quad(p_i \;is \;a \;prime).\]
那么，根据乘法计数原理，显然有\(\sigma{(n)} = (1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1}) \cdot (1 + p_2^1 + p_2^2 + \cdots + p_2^{\alpha_2}) \cdot (1 + p_3^1 + p_3^2 + \cdots + p_3^{\alpha_3}) \cdot \,\, \cdots \,\, \cdot (1 + p_n^1 + p_n^2 + \cdots + p_n^{\alpha_n})\).

正难则反，我们不方便研究\(\sigma{(n)}\)为偶数的情况，我们可以研究\(\sigma{(n)}\)为奇数的个数，然后用总数减掉奇数个数，就得到偶数个数。

1. 首先，我们要清楚

• 偶数 + 偶数 = 偶数
  奇数 + 偶数 = 奇数
  奇数 + 奇数 = 偶数

• 偶数 * 偶数 = 偶数
  奇数 * 偶数 = 偶数
  奇数 * 奇数 = 奇数。

1. 我们知道，只有让\(\sigma{(n)}\)的全部因数都为奇数才可以使\(\sigma{(n)}\)为奇数。

• 若\(2 \,| \,n\)，则\((1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1})\)这项一定是奇数。因为\(2\)的任何次幂都是偶数，且偶数 + 奇数 = 奇数。

• 对于除\(2\)以外的其他质数，它的任何次幂都一定是奇数。要想使因数项为奇数，则只能构造($1 + $ 偶数) 的这种形式.当有偶数个奇数相加时，它们的和是偶数。所以，\(\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n\)（不包括\(2\)的指数）都应该是偶数。

• \(n\) 可以是一个完全平方数。当\(n\)是一个完全平方数时，\(\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n\)都是偶数。因为\(n\)可以找到两个完全相同的因子。
  或者，\(n\)可以是$2 \times $ 完全平方数。因为把\(2\)当作底数的因数项永远是奇数，所以乘上\(2\)依然能保持所有乘数项都是奇数。（为什么没有$2^2, 2^3, 2^4, \dots \times $ 完全平方数？当\(2\)的指数为偶数时，用完全平方数就可以找到这个数。如果是奇数时，指数 = 1 + 偶数，又还原为$2 \times $ 完全平方数。）

• 综上，\(ans = n - \sqrt{n} - \sqrt{n / 2}\)。

通过代码

/*
Problem
    LightOJ - 1336
Status
    Accepted
Time
    151ms
Memory
    2084kB
Length
    411
Lang
    C++
Submitted
    2019-11-26 23:30:58
RemoteRunId
    1641328
*/

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int main()
{
    int times, kase = 0;

    scanf("%d", &times);

    while(times --){
        ll n, cnt = 0;                //cnt也有可能会超过1e9，所以要声明为long long类型.
        scanf("%lld", &n);

        for(ll i = 1; i * i <= n; i ++){
            cnt ++;                 //不超过n的完全平方数计数.

            if(2 * i * i <= n)    
                cnt ++;             //不超过n/2的完全平方数计数.
        }

        printf("Case %d: %lld\n", ++ kase, n - cnt);
    }

    return 0;
}

Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

原文：https://www.cnblogs.com/satchelpp/p/11939382.html