LSTM和GRU

LSTM

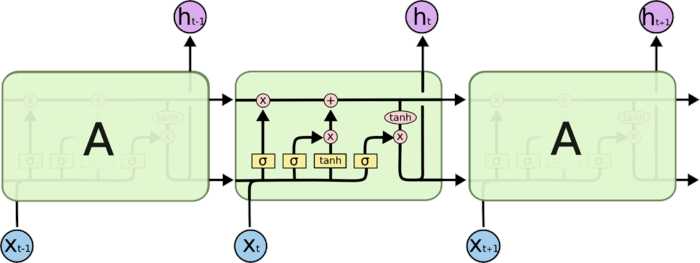
• 输入门\(i_t\):控制当前计算的新状态以多大的程度更新到记忆单元中
• 遗忘门\(f_t\):控制前一步记忆单元中的信息有多大程度被遗忘掉
• 输出门\(o_t\):控制当前的输出有多大程度取决于当前的记忆单元

• 记忆单元\(c_t\):每个单元都有

• 更新公式
  • 输入门：
    \[i_t=\sigma(W_ix_t + U_i h_{t-1} + b_i)\]
  • 遗忘门：
    \[f_t=\sigma(W_fx_t + U_f h_{t-1} + b_f)\]
  • 输出门：
    \[i_t=\sigma(W_ox_t + U_o h_{t-1} + b_o)\]
  • 记忆单元
    \[\tilde{c}_t=\tanh(W_c x_t + U_c h_{t-1})\]
  • 记忆单元更新：
    \[c_t=f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\]
  • 隐含层输出更新
    \[h_t=o_t \odot \tanh(c_t)\]
• 遗忘门和输入门控制着长短时记忆
• 更容易学习到序列之间的长期依赖
• 激活函数
  • 使用ReLU的话，难以实现门控效果
    • ReLU负半轴是关的，正半轴不具有门控意义
  • 在门控中，使用Sigmoid函数几乎是所有现代神经网络模块的共同选择
  • 计算能力有限设备，使用0/1门(hard gate)

GRU

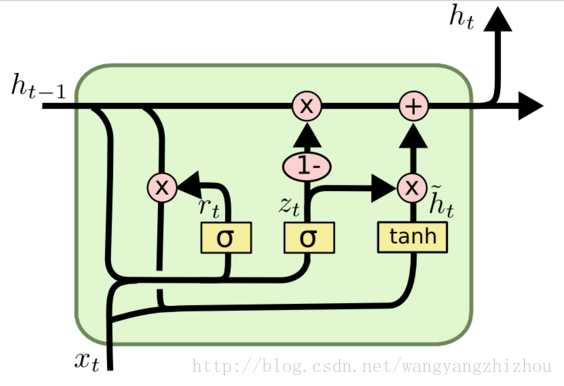
• 更新门\(z_t\):控制前一时刻的状态信息被带入到当前状态中的程度
• 重置门\(r_t\):控制忽略前一时刻的状态信息的程度
• 更新公式
  • 重置门：
    \[r_t=\sigma(W_r \cdot [h_{t-1}, x_t])\]
  • 更新门：
    \[z_t = \sigma(W_z \cdot [h_{t-1}, x_t])\]
  • 前一状态信息
    \[\tilde{h}_t=\tanh(W_h \cdot [r_t * h_{t-1}, x_t])\]
  • 隐状态
    \[h_t=(1-z_t)*h_{t-1} + z_t * \tilde{h}_t\]
• 其中\([]\)表示两个向量相连接，\(*\)表示矩阵元素相乘

LSTM和GRU比较

• GRU参数更少更简单，因此训练效率更高
• LSTM含有记忆单元，因此理论上更能记住长距离依赖
• 不是绝对的，与数据集相关，需要试验比较

LSTM和GRU

原文：https://www.cnblogs.com/weilonghu/p/11922994.html