一般用来进行误差值的表示、各种测量指标的表示,例如:准确率、精度、召回率等。下面举例:

在神经网络当中,向量更是十分的常见,例如神经元的偏置值b一般就要用向量来表示,这里的向量就是【b1,b2】T
例如我们现在要创建一个输入为5个结点,输出层为4个结点的线性网络层,那么此时创建的网络偏置值应该就是4维的,并且在TensorFlow中默认初始值为0:

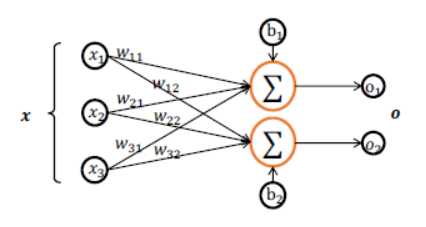
很多情况下会用到矩阵,最典型的就是权重的表示。例如我们创建一个线性网络层:
具体如下:
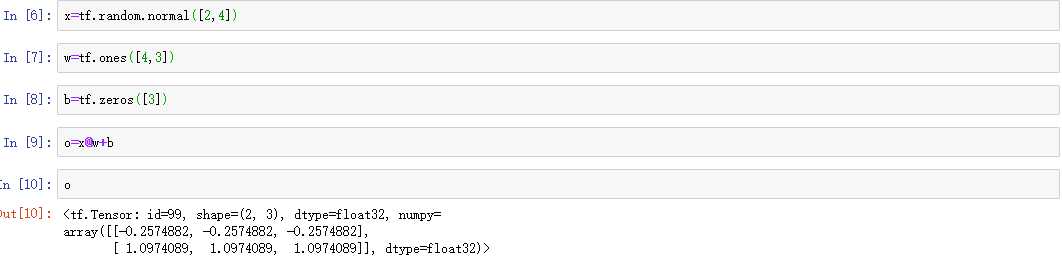
再例如,我们可以通过Dence方法创建一个网络层,然后通过kernel属性可以直接查看权重矩阵的形式,我们设计如下的网络层:输入4个结点,输出3个结点:
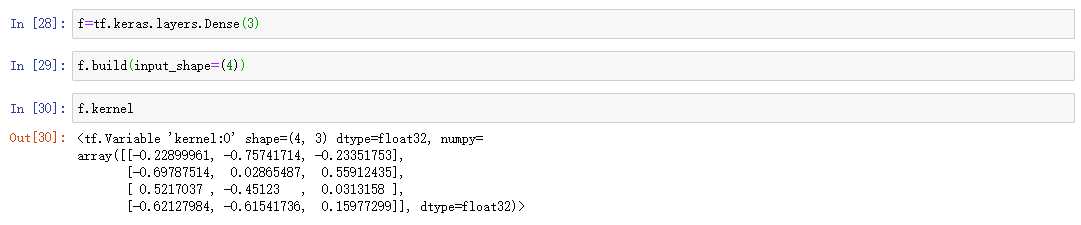
一般来讲:语义信息用三维张量表示,第一位表示句子个数,第二位表示句子的长度,第三位表示句子中单词的编码;图像信息用四维张量表示:第一位表示图像的数目,第二位、第三位表示图像的宽和高、第四位表示图像的通道数。
所谓索引就是获取某一个层面的张量的信息。有两种方式:
举例:我们对一张图像进行索引
第一种方法:
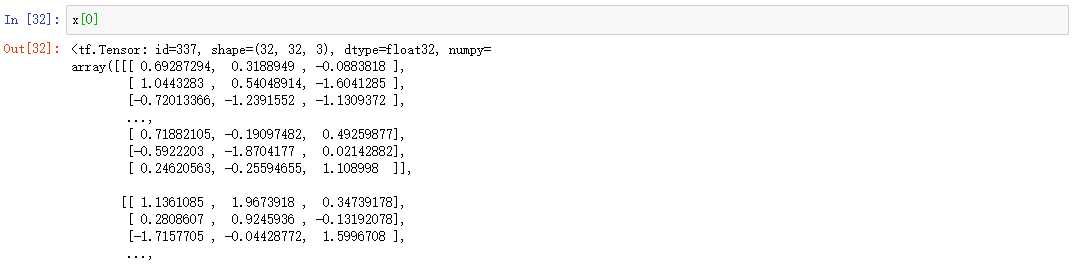
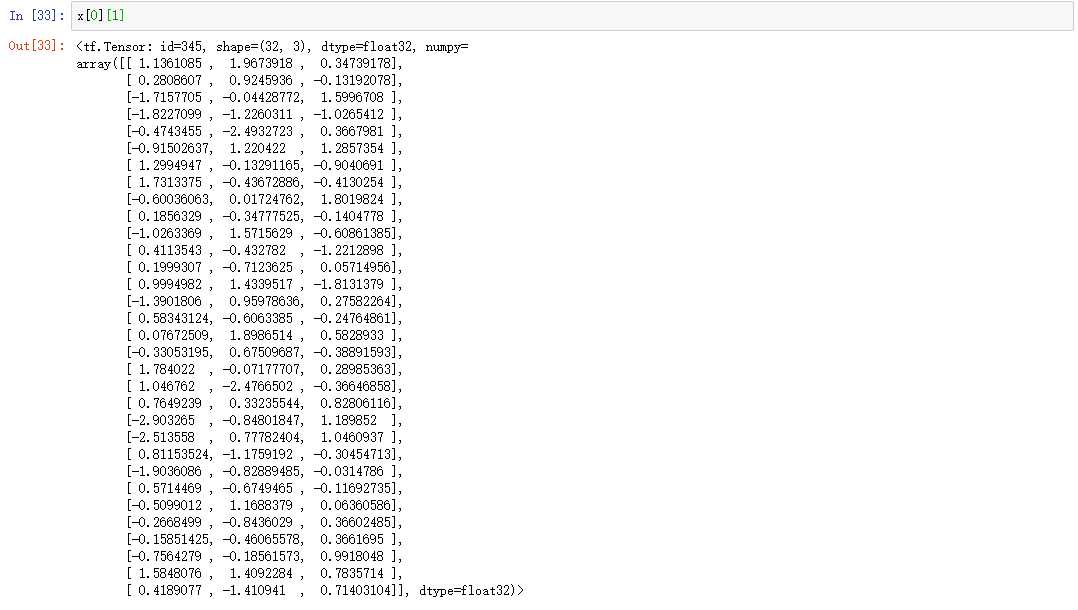

第二种方法:

所谓切片就是获取张量中某一个小部分的信息:
方法:通过【??????????: ??????: ????????】切片方式可以方便地提取一段数据,其中start 为开始读取位置的索引,end 为结束读取位置的索引(不包含end 位),step 为读取步长,步长为负数,表示逆序。
例如:现在获取某一图像张量的第2,3张图像的信息:

另外除了上面最标准的格式之外,我们还可以采用省略的方式,总结如下:

举例:
还有一种省略的写法如下:
现在我们想要获取所有图像中的G通道的图像信息,可以采用【:,:,:,1】这样的形式,也就看出来如果数据的维度太多,那么就会比较麻烦,写很多的冒号,因此出现省略号的写法,总结如下:

举例:
在神经网络当中有时我们需要将两个不同形状的张量进行加减操作,这个时候就要用到维度的变换。在TensorFlow当中,有改变视图reshape,插入新维度expand_dims,删除维度squeeze,交换维度transpose,复制数据tile等几种维度变换的方式。具体介绍如下:
这里主要是举例一个四维张量【2,4,4,3】的变化,特别需要注意的是我们可以改变张量的维度,但是有时候为了复现和数据还原等工作,我们必须考虑到不能随意改变内存当中张量的存储顺序,这一点应该尤其注意。
转换为【2,48】或者【2,-1】
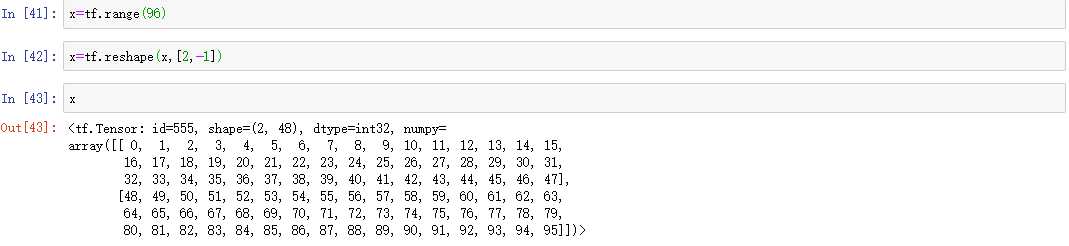
转换为【2,4,12】

转换为【2,16,3】
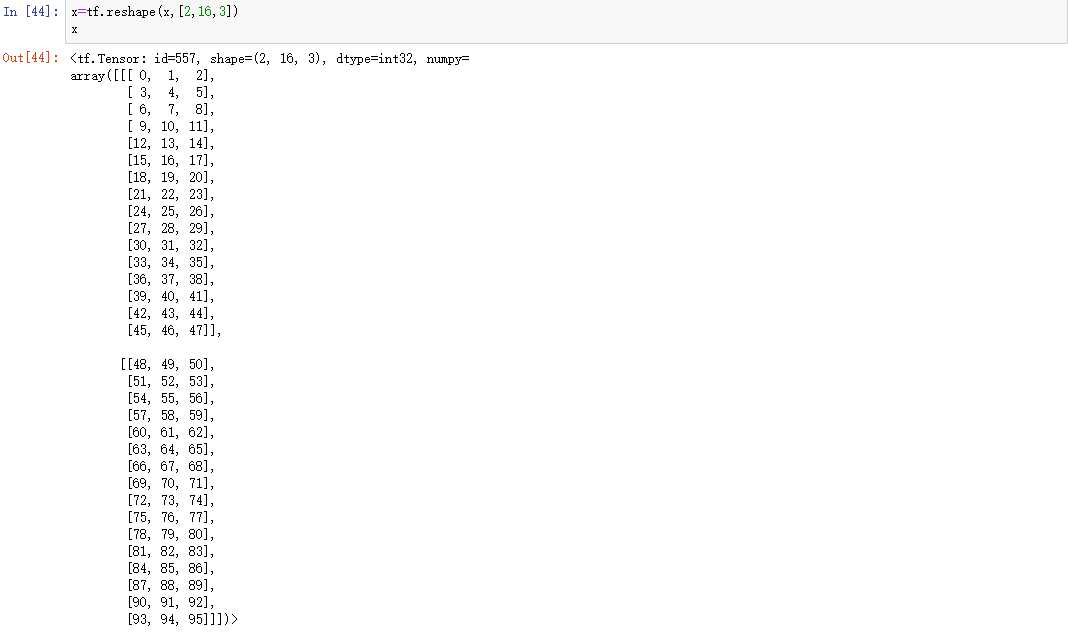
通过tf.expand_dims(x, axis)可在指定的axis轴前(注意当axis为正时表示在该轴之前,如果为负时表示在该轴之后)可以插入一个新的维度:
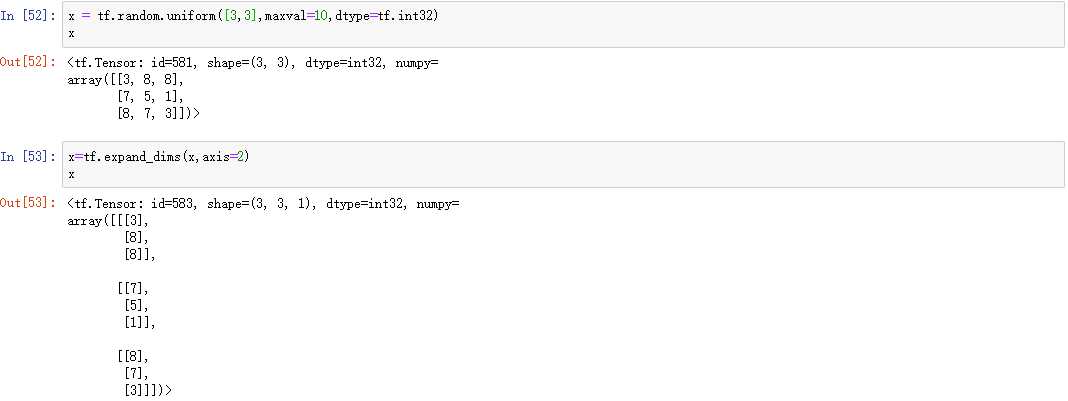
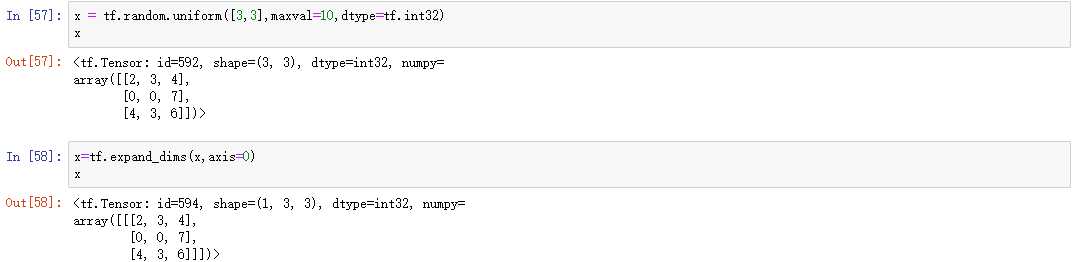
通过tf.squeeze(x, axis)函数,axis参数为待删除的维度的索引号(注意如果不指定索引号,默认删除大小为1的维度):
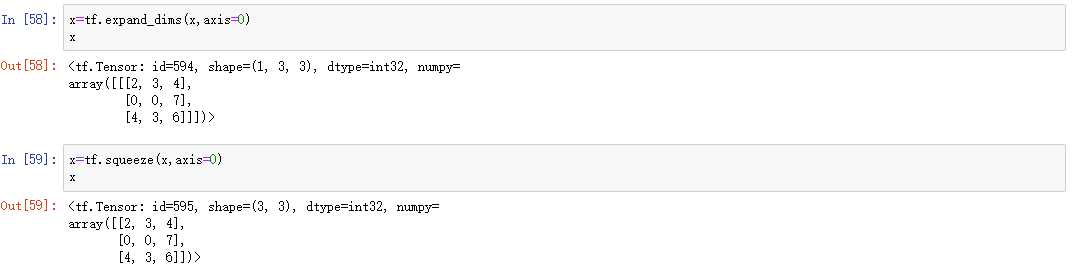
总结:上面谈到的维度变换的方法本质上是不改变数据的存储方式,但是会改变计算机对数据的理解方式,是对同样一堆有序列的数据的不同组织。
有时候为了适应某些以后的数据的组织形式,需要进行维度变换。
通过tf.transpose(x, perm)函数完成维度交换操作,其中perm 表示新维度的顺序List。
举例:考虑图片张量shape 为[2,4,4,3],图片数量、行、列、通道数的维度索引分别为0,1,2,3,如果需要交换为[??, ??, ?, ]格式,则新维度的排序为图片数量、通道数、行、列,对应的索引号为[0,3,1,2]:
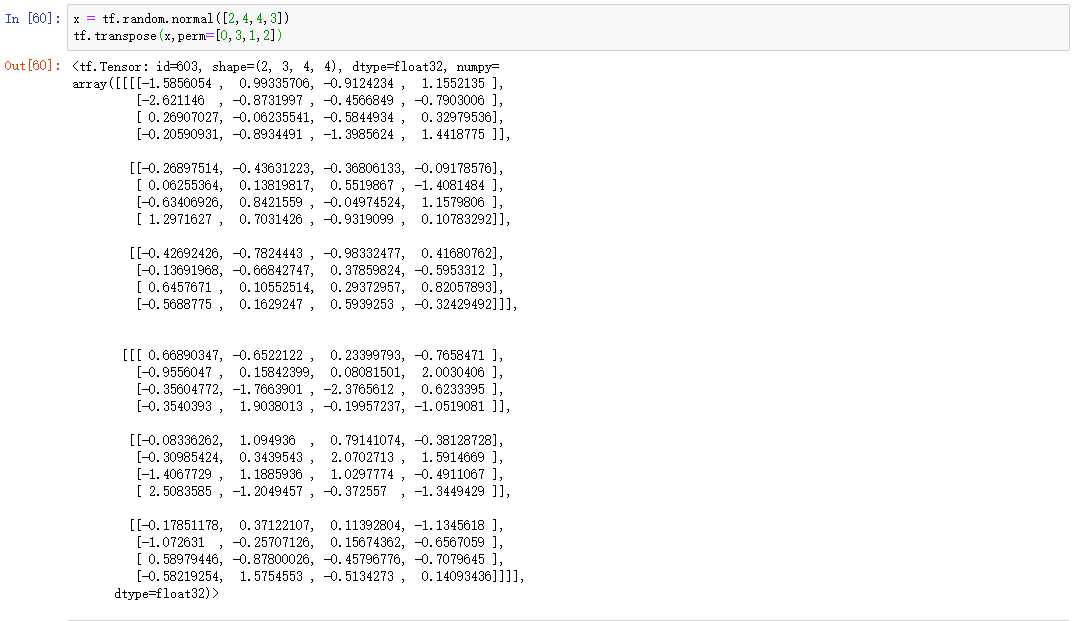
通过tf.tile(x, multiples)函数完成数据在指定维度上的复制操作,multiples 分别指定了每个维度上面的复制倍数,对应位置为1 表明不复制,为2 表明新长度为原来的长度的2 倍,即数据复制一份,以此类推。
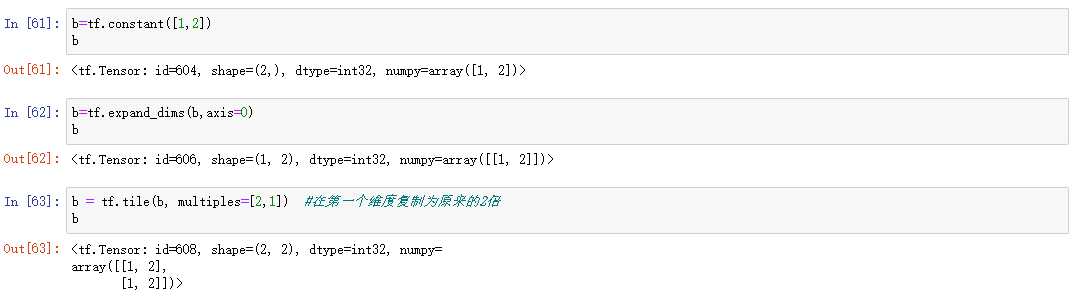
Broadcasting是TensorFlow中设计好的一种维度扩张机制,在上面的操作中,我们有时候为了可以实现相同shape的加减操作,我们需要将不符合要求的维度进行改变(主要就是维度插入和维度复制)后再进行操作,这是有些麻烦的,并且增加了计算量,于是产生了Broadcasting机制。
实现的步骤如下:
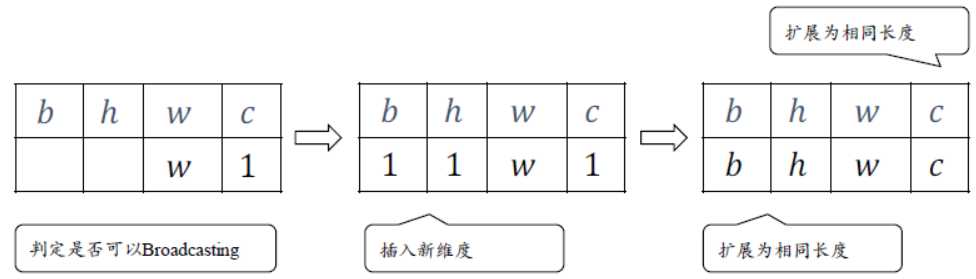
解释:
首先将2 个shape 靠右对齐,对于通道维度c,张量的现长度为1,则默认此数据同样适合当前维度的其他位置,将数据逻辑上复制?? − 1份,长度变为c;对于不存在的b 和h 维度,则自动插入新维度,新维度长度为1,同时默认当前的数据普适于新维度的其他位置,即对于其它的图片、其他的行来说,与当前的这一行的数据完全一致。这样将数据b,h 维度的长度自动扩展为b,h。
举例:
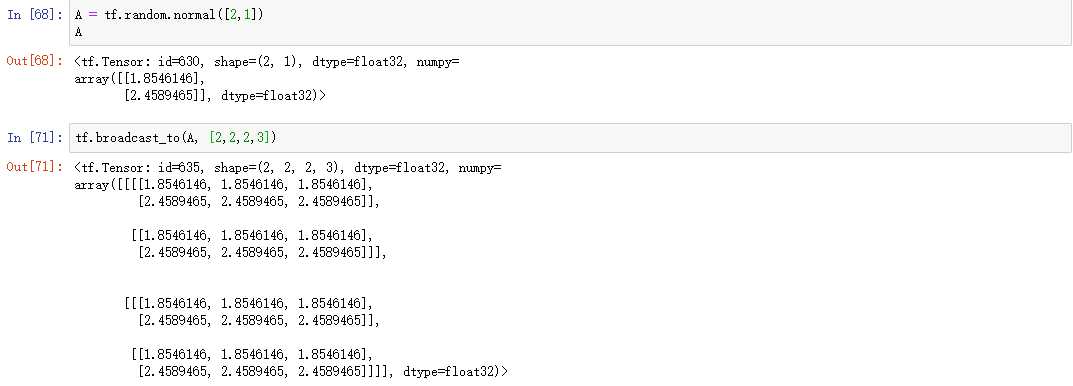
从上面的例子可以看出:Broadcasting机制的核心思想是普适性,即同一份数据能普遍适合于其他位置(原始A的第二个维度为1,结合上面的图理解也就是c=1)。
举一个不能适应的例子:

可能会想到,靠右对齐之后2可以扩张成4,但是2并不具备普适性,当要求的对象是3时则无法完成,所以体现了核心思想——普适性。
有了Broadcasting以后,那么下面的式子就可以直接运算,其中缘由也就理解了,纬度不同却可以正常相加:

原理图如下:
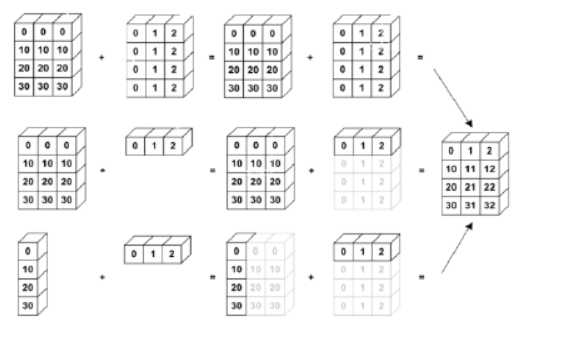
原文:https://www.cnblogs.com/lzy820260594/p/11896711.html