边长为\(1\)的正方形\(ABCD\)的顶点\(A,D\)分别在\(x\)轴,\(y\)轴的正半轴上滑动,则\(\overrightarrow{OB}\cdot \overrightarrow{OC}\)的最大值为\(\underline{\qquad\qquad}\).
解析:
如图,记\(E,F\)分别为\(AD,BC\)的中点,
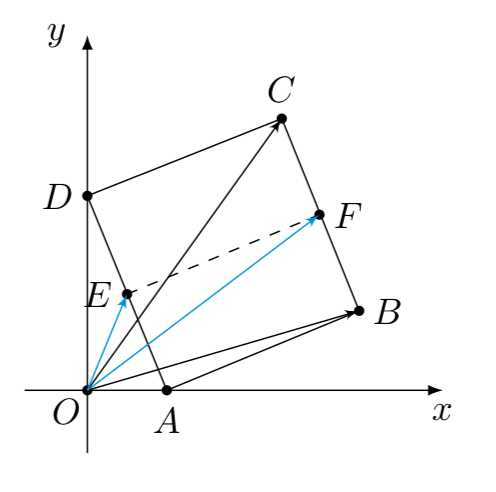
于是
\[
\begin{split}
\overrightarrow{OB}\cdot\overrightarrow{OC}&=\left(\overrightarrow{OF}+\overrightarrow{FC}\right)\cdot\left(\overrightarrow{OF}+\overrightarrow{FB}\right)\ &=|OF|^2-|FB|^2\ &=|OF|^2-\dfrac{1}{4}\ &\leqslant\left(|OE|+|EF|\right)^2-\dfrac14\ &= 2.
\end{split}
\]
当且仅当\(E\)点位于\(OF\)线段上时,上述不等式取等,因此所求表达式的最大值为\(2\).每日一题_191120
原文:https://www.cnblogs.com/Math521/p/11871556.html
