无约束问题定义如下：
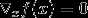
单约束问题定义如下：
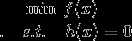
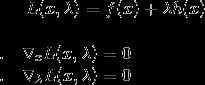
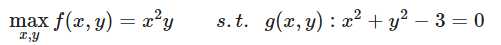
使用一个约束，一个拉格朗日乘子，得到拉格朗日函数：
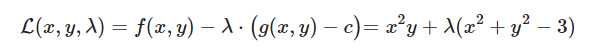
求导得到：
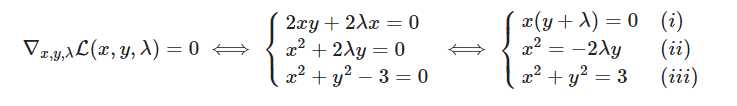
解得：
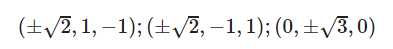
代入f（x， y）可得2， -2， 0， 也就是我们的最优值
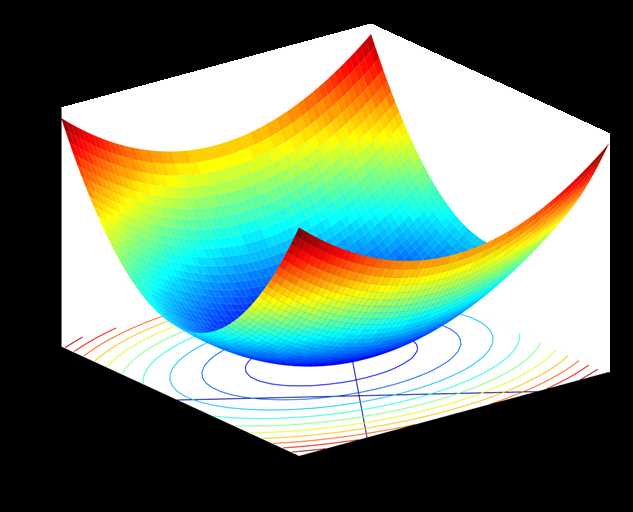
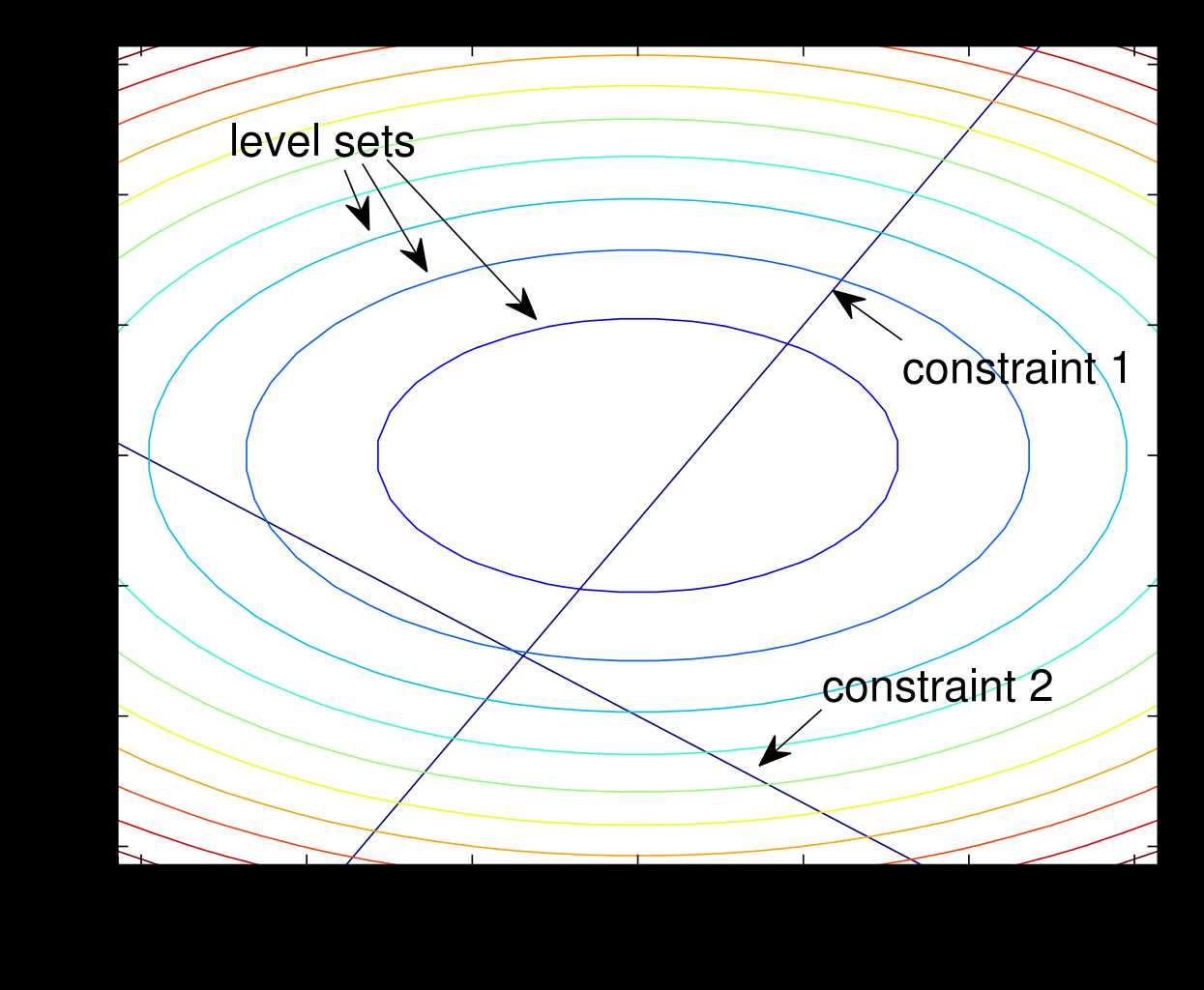
约束函数的即是一维空间的圆圈，变成目标函数的约束条件嵌入到目标函数的曲面中,整个过程如图:
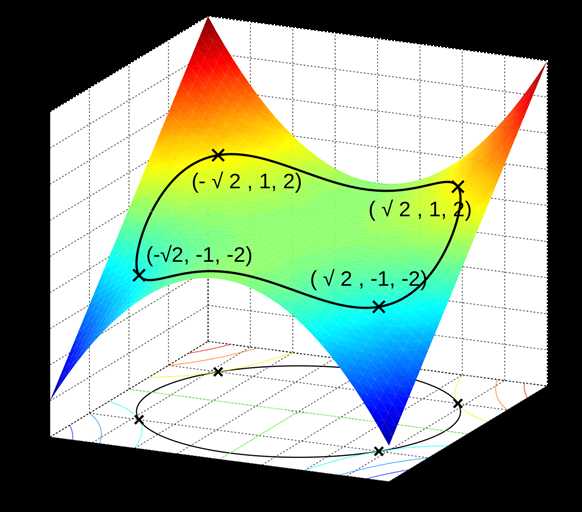
等式约束的多约束问题即有多个约束函数， 多约束问题的定义如下：
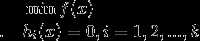
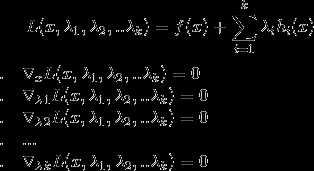
不等式问题单约束问题定义如下：
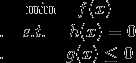
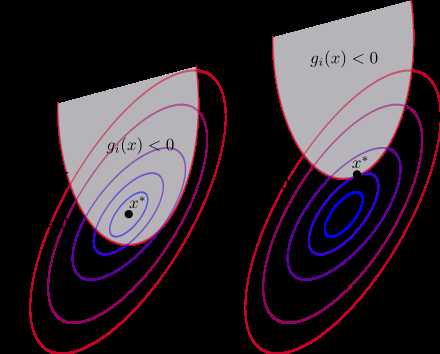
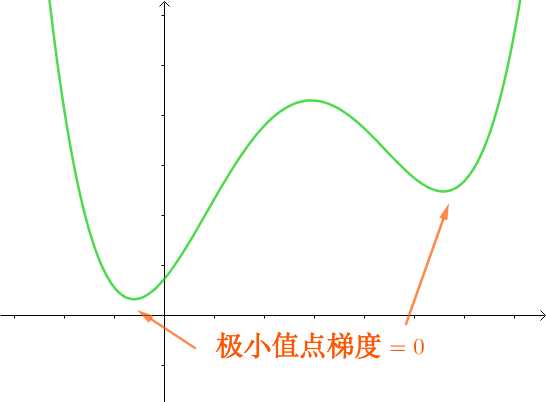
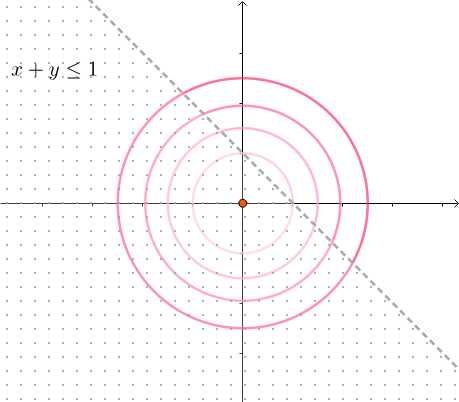
如图左，由于最优点在可行域内， 约束了跟没约束一样，由于等价于没有约束作用，所以直接可以对 f(x)+λh(x) 用拉格朗日乘子法
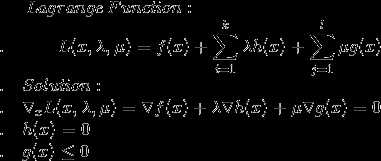
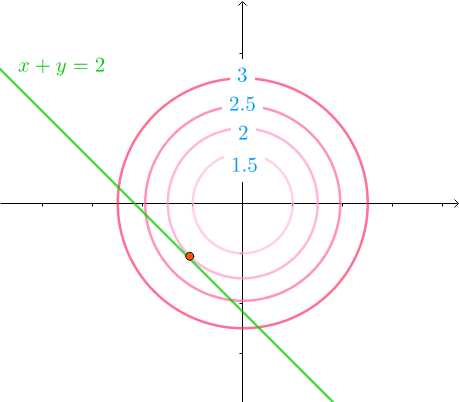
如图右，由于有约束的作用，约束条件最弱的时候取得最优值，可以看出， 最优解在可行域的边界上取得，转化成了等式约束，因此，不等式约束变成了等式约束。
（我也不想用可以看出的， 但是确实是这样，从等高图直观的来看， 可行域里面的等高更高，边界才有可能取得最优解）
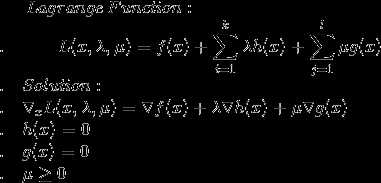
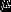大于 0 呢？后面通过例题来解释（先记住，俺也没咋搞懂， 老师跟我说这里很简单，但是他也记不得了，我搜了一堆博客，大部分都是用梯度解释的【惨兮兮）。
综上， 在情况一下，μ=0 且 g(x)≤0，情况二下，μ≥0 且 g(x)=0，将上面的条件综合起来， 写成多约束的形式，即可以得到大名鼎鼎的KKT条件：
.
.
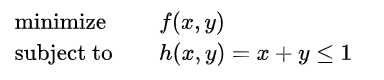
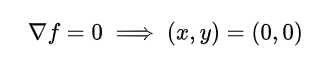
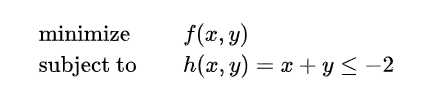
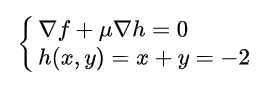
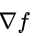的方向如下（法线也就是梯度，指向增长或下降最快的方向，这里用的是增长的， 也就是等高线的值变大的方向）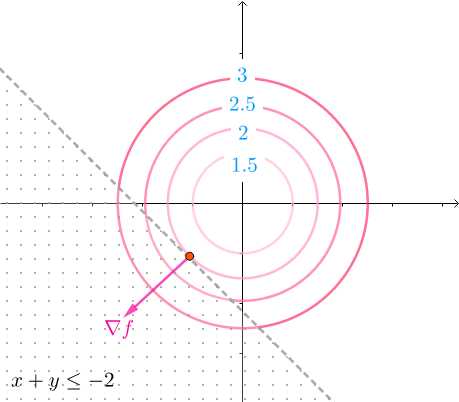
而凸函数h(x,y)的法线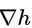
也一样指向h(x,y)增长的方向，这个方向正好和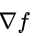相反：
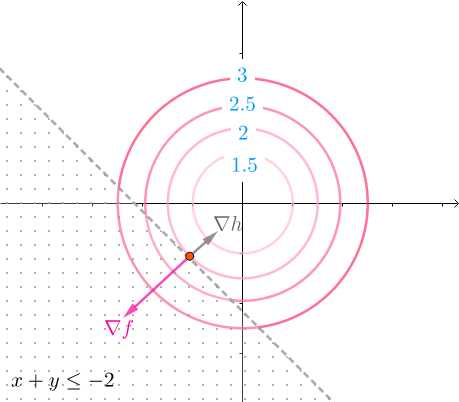
因此， 我们有
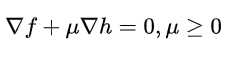
各个项以及对应的含义如下：
拉格朗日乘子（Lagrange multify）和KKT条件
原文：https://www.cnblogs.com/hichens/p/11863780.html