1.基本介绍
2.快速入门
给定集合val list = List(1, 2, 3, 4, "abc") ,要求将集合list中的所有数字+1,并返回一个新的集合,要求忽略掉非数字 的元素,即返回的 新的集合 形式为 (2, 3, 4, 5)
方式1:使用map和filter
object exercise_002 {
def main(args: Array[String]): Unit = {
val list = List(1, 2, 3, 4, "abc")
//思路1,使用map+fliter的思路
def f1(n:Any): Boolean = {
n.isInstanceOf[Int]
}
def f2(n:Int): Int = {
n + 1
}
def f3(n:Any): Int ={
n.asInstanceOf[Int]
}
val list2 = list.filter(f1).map(f3).map(f2)
println("list2=" + list2)
}
}
输出

这种方式虽然能够解决问题,但是显得繁琐
方式2:使用模式匹配
object exercise_003 {
def main(args: Array[String]): Unit = {
def addOne( i : Any ): Any = {
i match {
case x:Int => x + 1
case _ =>
}
}
val list = List(1, 2, 3, 4, "abc")
val list2 = list.map(addOne)
println("list2=" + list2)
}
}
输出

这种方式存在一个缺点是输出的序列中存在"()",然而还去不掉。
方式3:使用偏函数
object exercise_004 {
def main(args: Array[String]): Unit = {
def f2: PartialFunction[Any, Int] = {
case i: Int => i + 1 // case语句可以自动转换为偏函数
}
val list2 = List(1, 2, 3, 4,"ABC").collect(f2)
println(list2)
}
}
输出

上面的 val list2 = List(1, 2, 3, 4,"ABC").collect(f2)还可以进一步简化
val list3=List(1, 2, 3, 4,"ABC").collect{case i:Int => i+1}
3.偏函数是如何工作的呢?为了说明该问题,看如下实例
object exercise_005 {
def main(args: Array[String]): Unit = {
val list = List(1, 2, 3, 4, "abc")
val addOne3= new PartialFunction[Any, Int] {//使用匿名子类
def isDefinedAt(any: Any) = if (any.isInstanceOf[Int]) true else false
def apply(any: Any) = any.asInstanceOf[Int] + 1
}
val list3 = list.collect(addOne3)
println("list3=" + list3)
}
}
输出

执行过程解释:
collect函数的声明语句,可以发现它所接收的参数就是偏函数
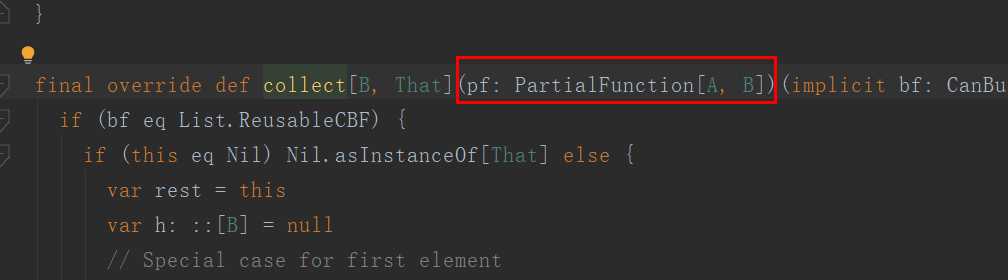
4.偏函数简化形式
声明偏函数,需要重写特质中的方法(isDefinedAt和Apply),有的时候会略显麻烦,而Scala其实提供了简单的方法。
“case语句可以自动转换为偏函数”,在上面的方式3中,我们使用的就是该特性。
函数作为一个变量传入到了另一个函数中,那么该作为参数的函数的类型是:function1,即:(参数类型) => 返回类型
看如下实例
def plus(x: Int) = 3 + x
val result1 = Array(1, 2, 3, 4).map(plus(_))
println(result1.mkString(","))
对于实例的说明
没有名字的函数就是匿名函数,可以通过函数表达式来设置匿名函数
val triple = (x: Double) => 3 * x println(triple(3))
说明
实例:编写一个匿名函数,可以返回2个整数的和,并输出该匿名函数的类型
object exercise_006 {
def main(args: Array[String]): Unit = {
val f1 = (n1: Int, n2: Int ) => {
println("匿名函数被调用")
n1 + n2
}
println("f1类型=" + f1)
println(f1(10, 30))
}
}
输出结果

能够接受函数作为参数的函数,叫做高阶函数 (higher-order function)。可使应用程序更加健壮。
实例1:定义一个高阶函数,参数能够接收函数和普通数据类型
object exercise_007 {
def main(args: Array[String]): Unit = {
//test 就是一个高阶函数,它可以接收f: Double => Double
def test(f: Double => Double, n1: Double) = {
f(n1)
}
//sum 是接收一个Double,返回一个Double
def sum(d: Double): Double = {
d + d
}
val res = test(sum, 6.0)
println("res=" + res)//12
}
}
高阶函数可以返回函数类型
def minusxy(x: Int) = {
(y: Int) => x - y //匿名函数
}
val result3 = minusxy(3)(5) //函数柯里化,先传入参数3,得到(y:Int)=3-y,再传入5,得到3-5=-2,最后返回计算结果
println(result3)
说明: def minusxy(x: Int) = (y: Int) => x - y
说明val result3 = minusxy(3)(5)
1.基本介绍
参数推断省去类型信息(在某些情况下[需要有应用场景],参数类型是可以推断出来的,如list=(1,2,3) list.map() map中函数参数类型是可以推断的),同时也可以进行相应的简写。
2.参数类型推断写法说明
3.实例:将集合中每个元素的值加上1,并返回值。观察演化过程
object exercise_009 {
def main(args: Array[String]): Unit = {
val list = List(1, 2, 3, 4)
println(list.map((x:Int)=>x + 1)) //(2,3,4,5)
println(list.map((x)=>x + 1))
println(list.map(x=>x + 1))
println(list.map(_ + 1))
val res = list.reduce(_+_)
}
}
说明
1. 基本介绍
2.函数柯里化快速入门
编写一个函数,接收两个整数,可以返回两个数的乘积,要求:
object exercise_010 {
def main(args: Array[String]): Unit = {
//说明
def mul(x: Int, y: Int) = x * y
println(mul(10, 10))
def mulCurry(x: Int) = (y: Int) => x * y
println(mulCurry(10)(9))
def mulCurry2(x: Int)(y:Int) = x * y
println(mulCurry2(10)(8))
}
}
输出结果

3.使用函数柯里化
比较两个字符串在忽略大小写的情况下是否相等,注意,这里是两个任务:
针对这两个操作,我们用一个函数处理的思想,其实也变成了两个函数处理的思想(柯里化)
方式1: 简单的方式,使用一个函数完成.
def eq2(s1: String)(s2: String): Boolean = {
s1.toLowerCase == s2.toLowerCase
}
方式2:使用稍微高级的用法(隐式类):形式为 str.方法()
object exercise_011 {
def main(args: Array[String]): Unit = {
def eq(s1: String, s2: String): Boolean = {
s1.equals(s2)
}
implicit class TestEq(s: String) {
// 体现了将比较字符串的问题,分解成了两个任务完成
// 1.checkEq完成转换大小写
// 2.f函数完成比较任务
def checkEq(ss: String)(f: (String, String) => Boolean): Boolean = {
f(s.toLowerCase, ss.toLowerCase)
}
}
val str1 = "HellO"
print(str1.checkEq("HELLO")(_.equals(_)))
}
}
原文:https://www.cnblogs.com/cosmos-wong/p/11450661.html