本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
0 2 4 3
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15;
对于40%的数据:N<=100,M<=10000;
对于70%的数据:N<=1000,M<=100000;
对于100%的数据:N<=10000,M<=500000。保证数据随机。
对于真正 100% 的数据,请移步 P4779。请注意,该题与本题数据范围略有不同。
样例说明:
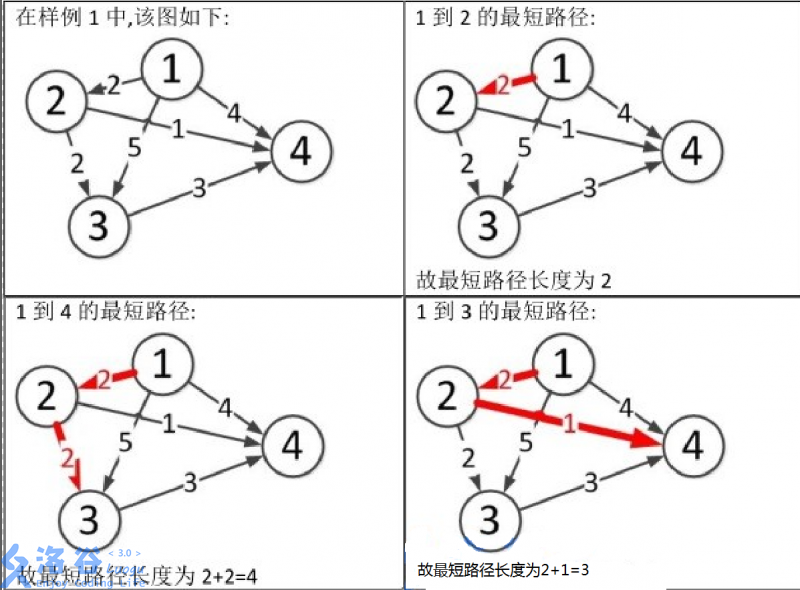
图片1到3和1到4的文字位置调换
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
long long dis[10001];
int u[500001],v[500001],w[500001],n,m,s,check;
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u[i],&v[i],&w[i]);
}
for(int i=1;i<=n;i++){
dis[i]=2147483647;
}
dis[s]=0;
for(int k=1;k<=n-1;k++){
check=0;
for(int i=1;i<=m;i++){
if(dis[v[i]]>dis[u[i]]+w[i]){
dis[v[i]]=dis[u[i]]+w[i];
check=1;
}
}
if(check==0){
break;
}
}
for(int i=1;i<=n;i++){
printf("%d ",dis[i]);
}
return 0;
}
原文:https://www.cnblogs.com/xiongchongwen/p/11858806.html