支持向量机(support vector machines ,SVM)是一种定义在特征空间上的间隔最大的二类分类模型。
?
线性可分支持向量机
假定特征空间上的训练数据集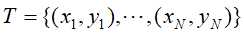 ,其中
,其中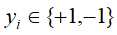 ,支持向量机的学习目标是找到一个超平面
,支持向量机的学习目标是找到一个超平面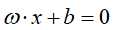 将训练数据集分为两个部分,并且是数据集中的点到这个超平面的几何间隔最大。
将训练数据集分为两个部分,并且是数据集中的点到这个超平面的几何间隔最大。
至此,支持向量机的线性学习可转化为以下的最优化问题:
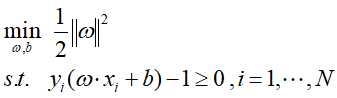
例子:如下图1-1中的训练数据集,正例点是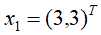 ,
,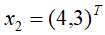 ,负例点是
,负例点是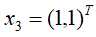 ,试求最大间隔分离超平面。
,试求最大间隔分离超平面。
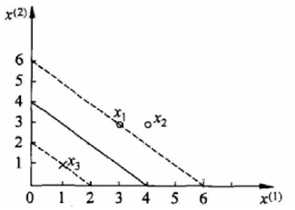
图1-1 间隔中最大分离超平面示例
?
解:根据训练集构造约束条件最优化问题:
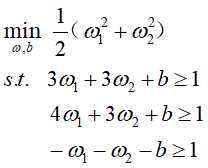
由此解得使间隔最大化的超平面为: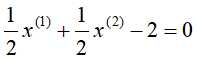 ,其中
,其中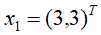 和
和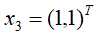 为支持向量(训练数据集中与分离超平面距离最近的样本点的实例)。对应的决策函数为:
为支持向量(训练数据集中与分离超平面距离最近的样本点的实例)。对应的决策函数为: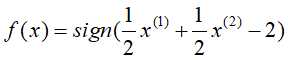 。
。
为了求解线性可分支持向量机的最优化问题,应用拉格朗日对偶,将上述的原始最优化问题转化为通过求解对偶问题得到最优解,这种转化为通过对偶问题求解可使得其最优解更容易被求得,也使得其更容易引入核函数,进而推广到非线性的分类问题上。
引入拉格朗日乘子得:
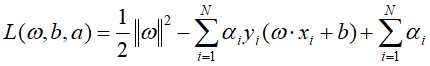
据拉格朗日对偶性,原始问题对偶问题是极大极小问题: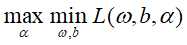
首先求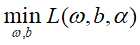 ,即将拉格朗日函数
,即将拉格朗日函数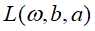 分别对
分别对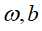 求偏导数并令其为0,然后将求得的结果代回
求偏导数并令其为0,然后将求得的结果代回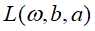 ,得:
,得:
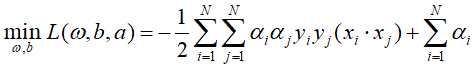
再求 对
对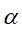 的极大化,等价于目标函数
的极大化,等价于目标函数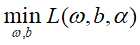 的负值对
的负值对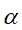 的极小化,即是对偶问题:
的极小化,即是对偶问题:
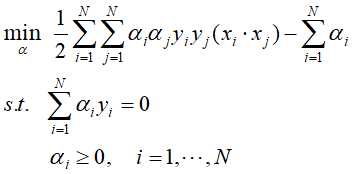
假设经过计算得到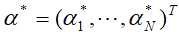 是这对偶问题的最优解,则
是这对偶问题的最优解,则
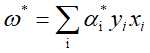
并选择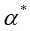 中的一个正分量
中的一个正分量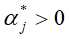 ,计算
,计算
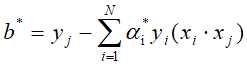
进而得分离超平面为: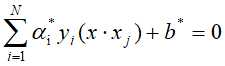 ,分类决策函数:
,分类决策函数: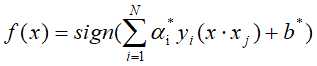
?
线性支持向量机
上述的支持向量机是在线性可分的基础条件上得出,而实际中,训练数据集中往往会存在一些噪点使得数据集不是线性可分的,对此需要对上述的支持向量机做出一些修改,即增加正则化项,将硬间隔化为软间隔,使得其也能够支持线性不可分的情况。
具体地,为每一个样本引入松弛变量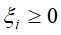 和一个大于0的惩罚参数
和一个大于0的惩罚参数 ,那么线性不可分的线性支持向量机的学习问题变成凸二次规划问题:
,那么线性不可分的线性支持向量机的学习问题变成凸二次规划问题:
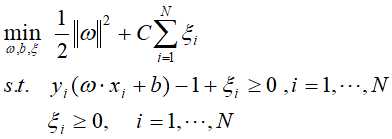
同样,将上述的问题转换为对偶问题:
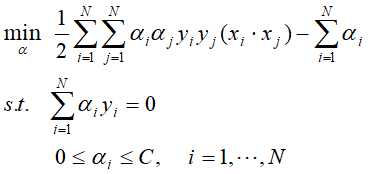
接下来的求最优解的步骤与上面的可线性划分支持向量机的相似。
假设经过计算得到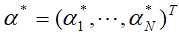 是这对偶问题的最优解,则
是这对偶问题的最优解,则
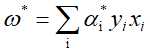
并选择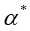 中的一个分量
中的一个分量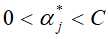 ,(这里选择分量与上面的区别开)计算
,(这里选择分量与上面的区别开)计算
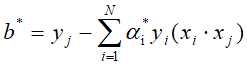
进而得分离超平面为: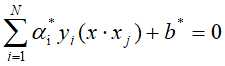 ,分类决策函数:
,分类决策函数: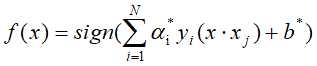
?
非线性支持向量机
对于非线性可分的问题,则利用核技巧,将非线性分类问题变换为线性分类问题。(核技巧的基本思想是通过一个非线性变换将输入空间对应于另一个特征空间,使得输入空间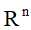 中的超曲面模型对应于特征空间
中的超曲面模型对应于特征空间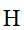 中的超平面)
中的超平面)
将线性支持向量机中对偶问题目标函数的内积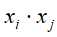 用内核
用内核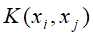 来代替,而求最优解的步骤与上面的线性支持向量机的类似:
来代替,而求最优解的步骤与上面的线性支持向量机的类似:
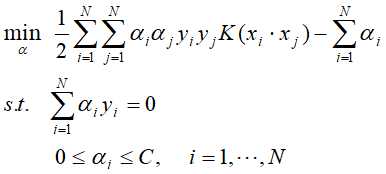
假设经过计算得到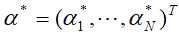 是这对偶问题的最优解,选择
是这对偶问题的最优解,选择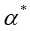 中的一个分量
中的一个分量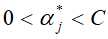 ,(这里选择分量与上面的区别开)计算
,(这里选择分量与上面的区别开)计算
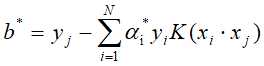
进而得分离超平面为: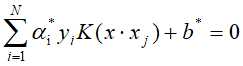 ,分类决策函数:
,分类决策函数: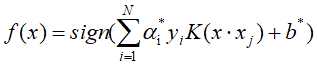
原文:https://www.cnblogs.com/lincz/p/11789882.html