今天尽可能详细的阐述此问题,探究其本质
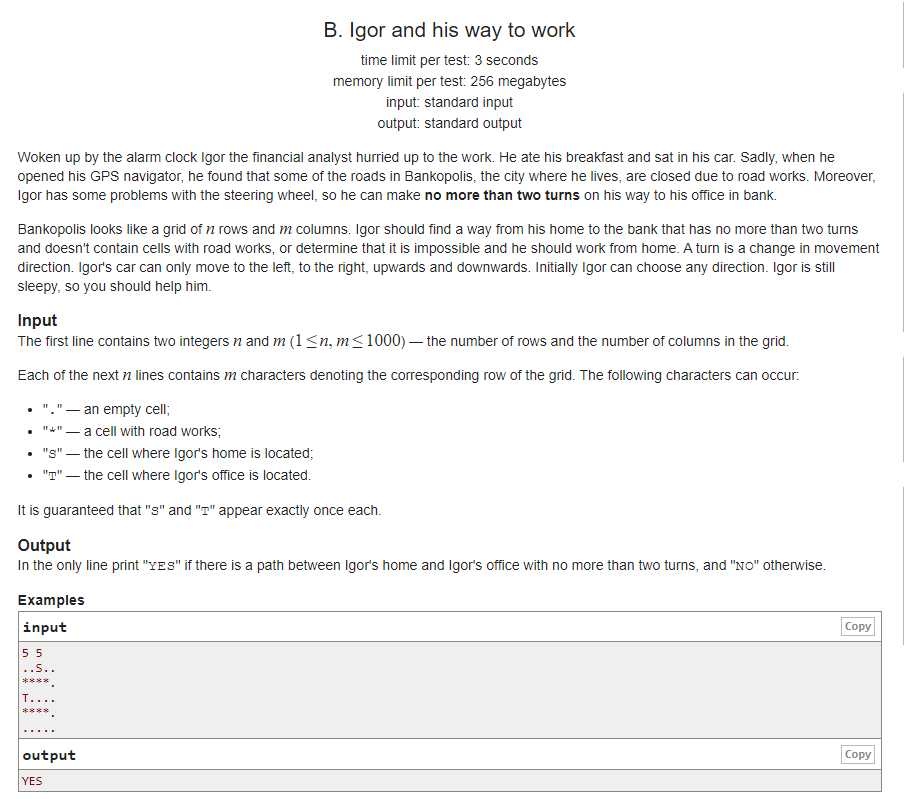
题意转两次弯是否能从S点到达T点?
错误源码:
#include <iostream>
#include <cstring>
#include <string>
//#include <map>
#include <queue>
using namespace std;
int a[1001][1001];
bool bo[1001][1001];
int fx[][2] = { {-1,0},{1,0},{0,-1},{0,1} };
int x1, y11, x2, y2, n, m;
struct node {
int x, y, step;
};
queue <node> q;
int main()
{
cin >> n >> m;
char ch;
for (int i = 1; i <= n; i++)
{
cin.sync();
for (int j = 1; j <= m; j++)
{
cin >> ch;
if (ch == ‘.‘) a[i][j] = 1;
else if (ch == ‘*‘) a[i][j] = 0;
else if (ch == ‘S‘) {
x1 = i; y11 = j;
a[i][j] = 1;
}
else if (ch == ‘T‘) {
x2 = i; y2 = j;
a[i][j] = 1;
}
}
}
node tmp;
tmp.x = x1; tmp.y = y11; tmp.step = -1;
q.push(tmp);
bo[x1][y11] = true;
while (!q.empty() && q.front().step<=1)
{
node tmp2 = q.front(); tmp2.step = q.front().step+1;
q.pop();
int tx = tmp2.x; int ty = tmp2.y;
for (int i = 0; i < 4; i++)
{
tmp2.x = tx+fx[i][0]; tmp2.y = ty+fx[i][1];
while (tmp2.x > 0 && tmp2.y > 0 && tmp2.x <= n && tmp2.y <= m && !bo[tmp2.x][tmp2.y] && a[tmp2.x][tmp2.y] != 0)
{
q.push(tmp2);
bo[tmp2.x][tmp2.y] = 1;
tmp2.x += fx[i][0]; tmp2.y += fx[i][1];
}
}
}
if (bo[x2][y2]) cout << "YES" << endl;
else cout << "NO" << endl;
return 0;
}
类似于染色问题的朴素宽搜。一直WA第7个点。
直到此数据让我知道天才的我为什么会wa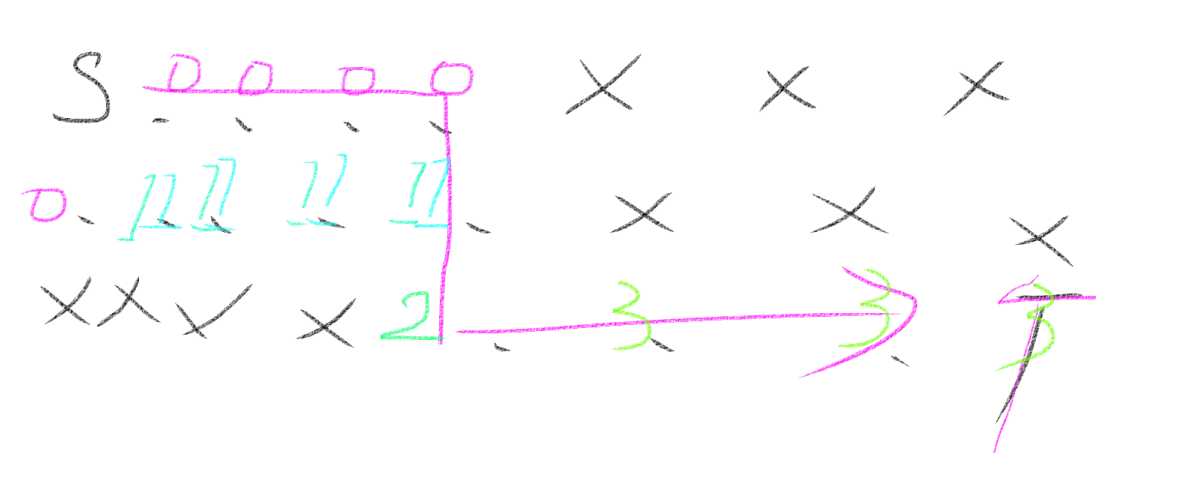
由于采用了不重复的剪枝,处理过一个点后会把此点染色,变为非通路(相当于施工中)(也就是杀点,设路障以剪枝)。那么(1,5)的就无法正常到达(3,5)。导致WA。
由于染色等问题是向周围的点扩散,所以并没有所谓的“后遍历到的点其实是最优解,却因为剪枝而无法覆盖”的问题。所以保证了先BFS到的点一定为最优解。
而这里存在问题是因为,“”(我也不知道啊卧槽)______>垃圾见解:同一层级,比如(1.5)的step=0的点可以一直延申到(3,5)时保持step=1。却因为先遍历了step=0时的(2,1),而导致(1,5)被提前染色而变为非通。所以最优解就被杀了。
问题的本质在于染色(杀点,也就是设为路障)的时机。应该在同一层(比如step=0,step=1,step=2)全部结束后进行染色,而非单步染色。
因为平时解决的bfs模板题, 都是单步为一层的,比如走迷宫类型的最短路径,每过一个点step++,同时染色,看起来就没问题了。
------------------------------------------------------------------------------------------------------已经有复数的同学搜了题解了,很不幸这是我,本人,今天提了AF的蒟蒻写的题解,并且未完成---------------------------------------------------
顺便记一下debug
我的解法,
#include <iostream>
#include <cstring>
#include <string>
#include <queue>
using namespace std;
struct node {
int x, y, step;
};
queue <node> q;
int ans[1001][1001];
int n, m;
int ax, ay;
int bx, by;
const int fx[][2] = { {-1,0},{1,0},{0,-1},{0,1} };
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin.sync();
for (int j = 1; j <= m; j++)
{
char ch;
cin >> ch;
if (ch == ‘.‘) ans[i][j] = 9;
else if (ch == ‘*‘) ans[i][j] = -2;
else if (ch == ‘S‘) {
ans[i][j] = -1;
ax = i; ay = j;
}
else if (ch == ‘T‘)
{
ans[i][j] = 9;
bx = i; by = j;
}
}
}
node tmp;
tmp.x = ax; tmp.y = ay;
q.push(tmp); int s = 0;
while (!q.empty() && s<=2) {
node temp;
temp = q. front(); q.pop();
s = ans[temp.x][temp.y] + 1;//更新层数
for (int i = 0; i < 4; i++) //尝试从此点出发向上下左右直行
{
int x = temp.x + fx[i][0], y = temp.y + fx[i][1];
while (x > 0 && x <= n && y > 0 && y <= m && ans[x][y] >= s)
{
node tmp2;
tmp2.x = x; tmp2.y = y;
ans[x][y] = s;
if (s<2) q.push(tmp2); //剪枝防止爆内存,s=2时就不需要入队等他拐第三个弯了
x += fx[i][0]; y += fx[i][1];
/* cout << endl;//调试
for (int i = 1; i <= n; i++)
{
cout << endl;
for (int j = 1; j <= m; j++)
printf_s("%3d", ans[i][j]);
}*/
}
}
}
if (ans[bx][by] <= 2) cout << "YES" << endl;
else cout << "NO" << endl;
return 0;
}
如果在队列中记step的话,有可能重点不重step,这时候就要打补丁去重……
如果加一个bool判断是否要杀点的话,只有0,1,而这里优先级不同,bool判断不过来。
所以直接删掉所有碍事的东西,只留一个ans数组。
同一层级相同优先,如果目标cell的值比当前层级小就不要考虑了,相当于被杀点,(因为你没法把最优解换成傻逼解) 如果比当前层级大的话就更新为最优解(BFS一定是最优解!)
然而等于相同层级呢?
相同层级的问题相同优先,因为都是最优解,所以可覆盖,也不存在A挡住了B的问题妨碍B继续播撒DNA。
所以除了判断边界,只留了一个逻辑判断是否更新最优解(看!不是更新染色,有区别)。
tips,如果把>=换成>,那么和源码1一样,都错第7点(原理一样的呜呜呜)
---------------------------------------------------------------------------------------------------------------------------------------------------------------
感谢hxr:这种情况下bfs和dfs就没区别了;
感谢ml:
你要更新最优解,bfs保证距离最短,不能保证转弯少。
↑:我的思路源泉
原文:https://www.cnblogs.com/asanagiyantia/p/11780295.html