左偏树是用来快速地合并堆的
正常的堆是一颗完全二叉树,我们用笨方法去合并它:
假设我们要将x和y这两个小根堆合并,我们判断一下如果x的堆顶大于y的堆顶,就交换一下x和y,然后继续合并x的某个子孩子和y。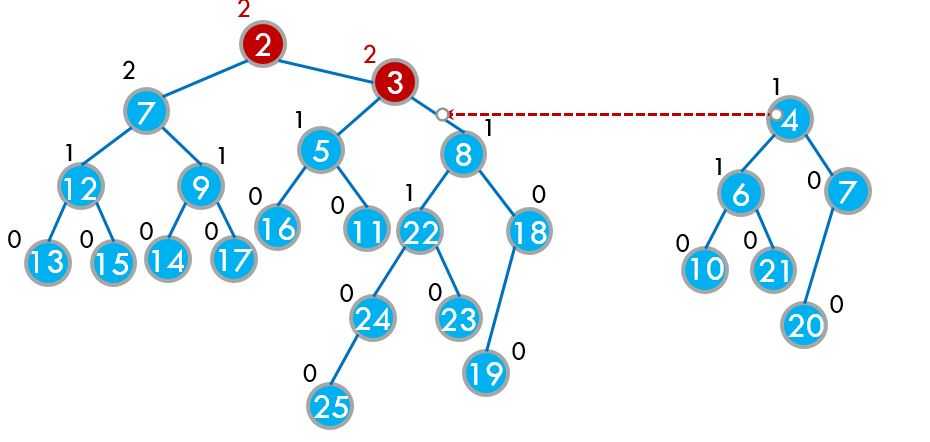
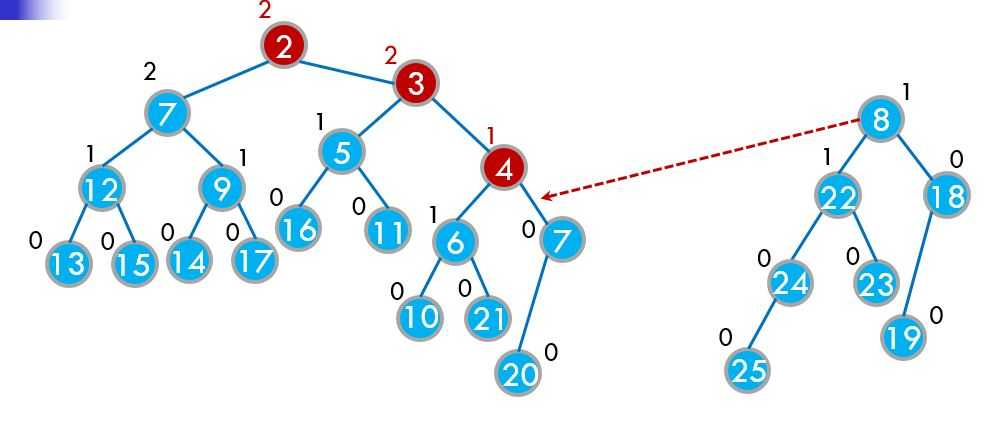
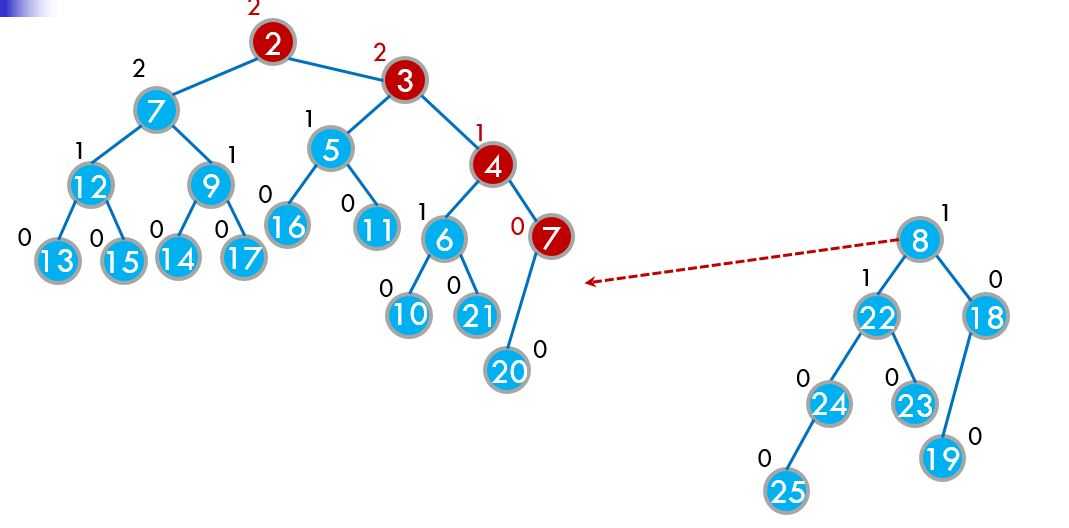
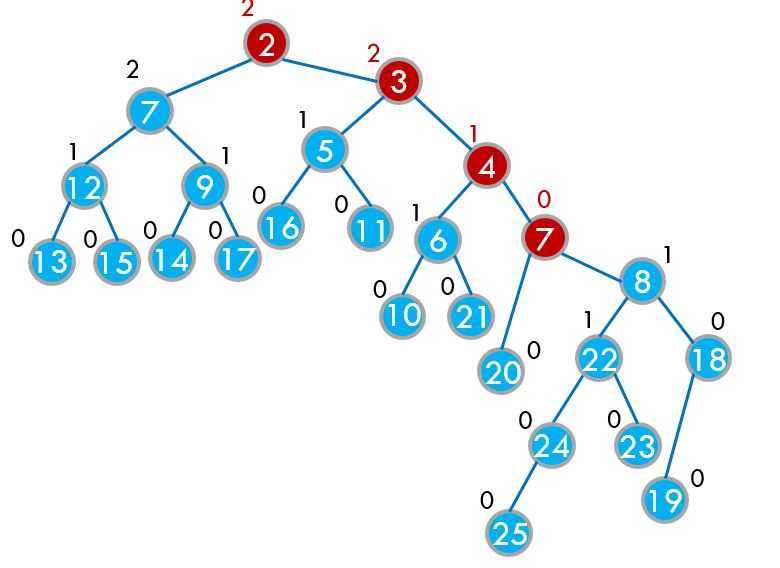
堆被人们所推广的原因就是因为它的时间复杂度比较稳定,根本原因是堆是一颗完全二叉树
但显然的:这样合并堆并没有保证时间复杂度,也就是说没有维护完全二叉树的形态;
这时候解决的办法之一便是利用左偏树;
它比普通的堆多了一个性质:向左偏;
注意,这里的向左偏并不是指子树的大小向左偏,而是最大深度向左偏;
为了方便我们理解,我们引入一下几种概念:
我们这里定义一个值,叫做"根值",一个节点的根值就是它到最近的叶子节点的距离;
我们保证,任意一个节点的左儿子的根值大于等于右儿子的根值;
这样我们会得到一个性质:
一个n个节点的左偏树距离最大为log(n+1)−1
简易论证:
若左偏树的根值为一定值,则节点数最少的左偏树是完全二叉树
若一棵左偏树的距离为k,则这棵左偏树至少有2^(k+1)-1个节点;
这样做的时间复杂度是O(logn),我们可以接受;(并且没用STL,常数也很小)
为了更加的优化程序,我们可以使用路径压缩来快速找到每个元素属于哪个根
#include <bits/stdc++.h>
#define inc(i,a,b) for(register int i=a;i<=b;i++)
using namespace std;
int n,m;
int dis[1000010],root[1000010],lson[1000010],rson[1000010];
template<class nT>
inline void read(nT& x)
{
char c;while(c=getchar(),!isdigit(c));
x=c^48;while(c=getchar(),isdigit(c)) x=x*10+c-48;
}
struct node{
int pos;
int value;
}tree[1000010];
int judge[10000010];
int find(int x)
{
if(root[x]==x){
return x;
}
return root[x]=find(root[x]);
}
int merge(int x,int y)
{
if(!x||!y) return x+y;
if(tree[x].value==tree[y].value){
if(tree[y].pos<tree[x].pos){
swap(x,y);
}
}
else if(tree[y].value<tree[x].value){
swap(x,y);
}
rson[x]=merge(rson[x],y);
if(dis[lson[x]]<dis[rson[x]]) swap(lson[x],rson[x]);
dis[x]=dis[rson[x]]+1;
return x;
}
int main()
{
dis[0]=-1;
cin>>n>>m;
inc(i,1,n){
read(tree[i].value);
root[i]=i; tree[i].pos=i;
}
inc(i,1,m){
int type,x,y;
read(type); read(x);
if(type==1){
read(y);
if(judge[x]||judge[y]) continue;
x=find(x); y=find(y);
if(x==y) continue;
root[x]=root[y]=merge(x,y);
}
else{
if(judge[x]){
cout<<"-1"<<endl;
}
else{
x=find(x);
cout<<tree[x].value<<endl;
judge[x]=1;
root[lson[x]]=root[rson[x]]=root[x]=merge(lson[x],rson[x]);
lson[x]=rson[x]=dis[x]=0;
}
}
}
}
原文:https://www.cnblogs.com/kamimxr/p/11779116.html