1、思路
应用Kmeans聚类时,需要首先确定k值,如果k是未知的,需要先确定簇的数量。其方法可以使用拐点法、轮廓系数法(k>=2)、间隔统计量法。若k是已知的,可以直接调用sklearn子模块cluster中Kmeans方法,对数据进行切割。
另外如若数据集不规则,存在量纲上的差异,也需要对其进行标准化处理。
2、数据的标准化处理
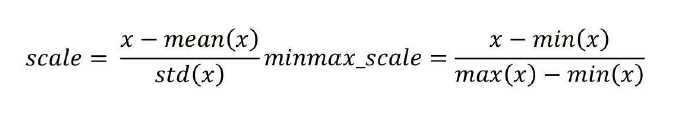
(minmax_scale为sklearn子模块processing 中 的函数),第一种方法为压缩变量为mean=0,std=1的无量纲数据,第二种方式会压缩变量为[0,1]之间无量纲数据 。
3、案例
1)对iris聚类(已知簇类的情况)
情况1,已知k值,k=3
调用KMeans模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from pylab import *
mpl.rcParams[‘font.sans-serif‘] = [‘SimHei‘]
iris = pd.read_csv(r‘iris.csv‘)
# 设置聚为3类,n_clusters =3
X = iris.drop(labels = ‘Species‘,axis = 1)
kmeans = KMeans(n_clusters =3 )
kmeans.fit(X)
X[‘cluster‘] = kmeans.labels_
X.cluster.value_counts()
# 绘制花瓣长度与宽度的散点图
import seaborn as sns
centers = kmeans.cluster_centers_
print(centers)
sns.lmplot(x = ‘Petal_Length‘,
y= ‘Petal_Width‘,
hue = ‘cluster‘,
markers = [‘^‘,‘s‘,‘o‘],
data = X,
fit_reg= False,
scatter_kws = {‘alpha‘:0.8},
legend_out = False
)
plt.scatter(centers[:,2], centers[:,3], marker = ‘*‘,color = ‘black‘, s =130) # 绘制簇中心点
plt.xlabel(‘花瓣长度‘)
plt.ylabel(‘花瓣宽度‘)
plt.show()
iris[‘Species_map‘] = iris.Species.map({‘virginica‘:0,‘setosa‘:1,"versicolor":2}) # 3种类型进行映射到0,1,2
sns.lmplot(x = ‘Petal_Length‘,
y= ‘Petal_Width‘,
hue = ‘Species_map‘,
markers = [‘^‘,‘s‘,‘o‘],
data = iris,
fit_reg= False,
scatter_kws = {‘alpha‘:0.8},
legend_out = False )
plt.xlabel(‘花瓣长度‘)
plt.ylabel(‘花瓣宽度‘)
plt.show()
生成图形如下:
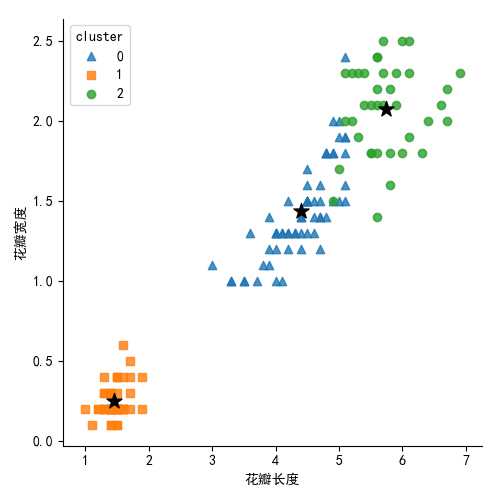
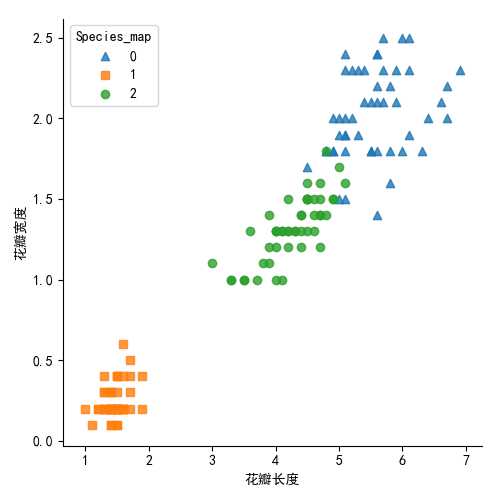
对簇中心做雷达图
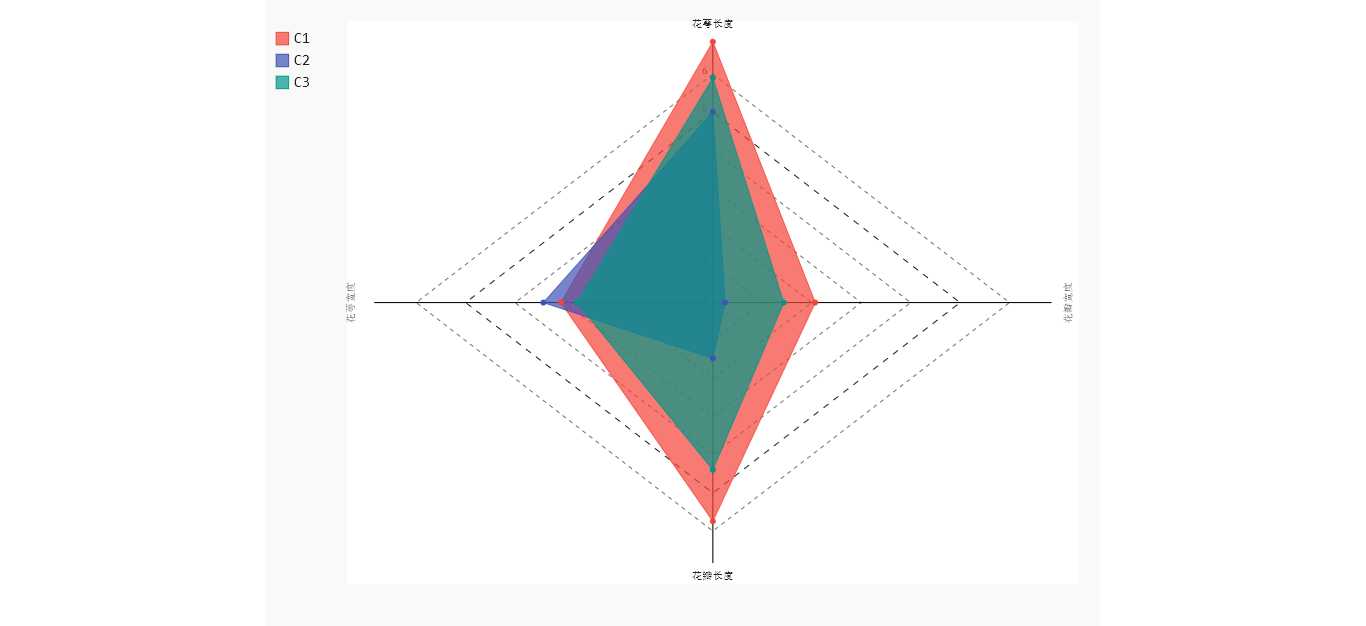
import pygal radar_chart = pygal.Radar(fill = True) radar_chart.x_labels = [‘花萼长度‘,‘花萼宽度‘, ‘花瓣长度‘,‘花瓣宽度‘] # 雷达图区域绘制 radar_chart.add(‘C1‘,centers[0]) radar_chart.add(‘C2‘,centers[1]) radar_chart.add(‘C3‘,centers[2]) radar_chart.render_to_file(‘radar_chart.svg‘)
生成如下图形,C1类型的花,花萼长和花瓣长都是最大的。C2类型的花,对应的3个指标值都比较小,C3类型的花,3个指标的平均值,恰好落在C1和C2之间。
2)NBA球员数据集聚类(未知k值)
数据集

选定得分、命中率,三分命中率,罚球命中率四个维度进行分析,观察数据情况,需进行标准化。
sns.lmplot(x = ‘得分‘,
y = ‘命中率‘,
data = players,
fit_reg = False,
scatter_kws = {‘alpha‘: 0.8,‘color‘: ‘steelblue‘}
)
plt.show()
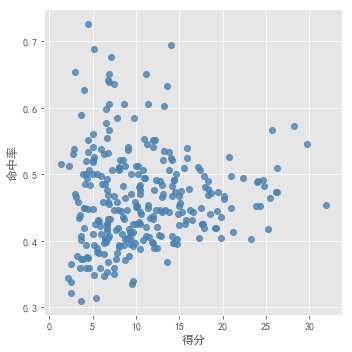
肉眼无法进行观察数据集适合分为几个簇。分别采用 以上确定k值的3种方法进行测试。
拐点法:
from sklearn import preprocessing X = preprocessing.minmax_scale(players[[‘得分‘,‘罚球命中率‘,‘命中率‘,‘三分命中率‘]]) # 数据集的标准化 X = pd.DataFrame(X, columns=[‘得分‘,‘罚球命中率‘,‘命中率‘,‘三分命中率‘]) k_SSE(X,15)
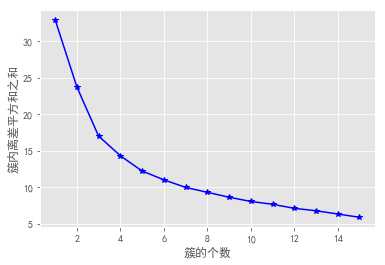
结果看出,k值在3、4斜率变化比较明显,在5以后斜率保持一定的水平。所以k取3,4,5均有可能。在比较其他方法。
轮廓系数法及Gap statistic法可视化效果如下:
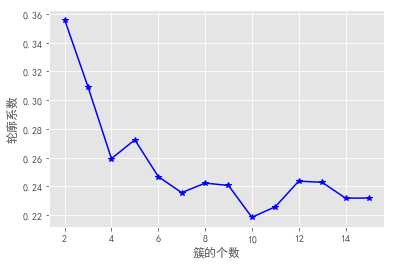
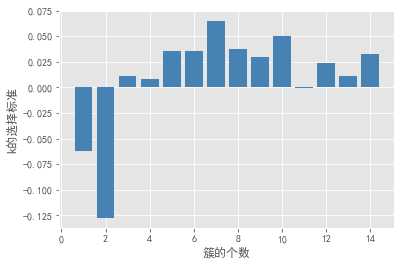
结合上图,轮廓系数在大于0的情况下,最大值对应的k值为2,统计量法首次出现正值的k值为3,综合考虑以上三种方法取k值为3,即将数据集分为3个簇最理想。
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
players[‘cluster‘] = kmeans.labels_
centers = []
for i in players.cluster.unique():
centers.append(players.ix[players.cluster == i, [‘得分‘,‘罚球命中率‘,‘命中率‘,‘三分命中率‘]].mean())
centers = np.array(centers)
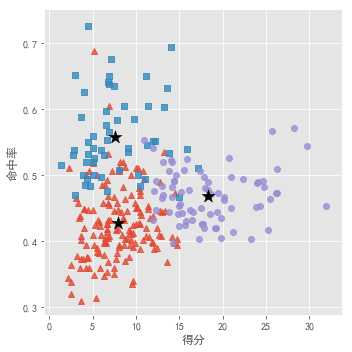
sns.lmplot(x = ‘得分‘,
y = ‘命中率‘,
hue = ‘cluster‘,
data = players,
markers = [‘^‘,‘s‘,‘o‘],
fit_reg = False,
scatter_kws = {‘alpha‘: 0.8},
legend = False
)
plt.scatter(centers[:,0],centers[:,2],c = ‘k‘,marker = ‘*‘,s =180)
plt.xlabel(‘得分‘)
plt.ylabel(‘命中率‘)
plt.show()
# 雷达图绘制
centers_std = kmeans.cluster_centers_
radar_chart = pygal.Radar(fill = True) # 设置填充型雷达图
radar_chart.x_labels = [‘得分‘,‘罚球命中率‘,‘命中率‘,‘三分命中率‘]
radar_chart.add(‘C1‘, centers_std[0])
radar_chart.add(‘C2‘, centers_std[1])
radar_chart.add(‘C3‘, centers_std[2])
radar_chart.render_to_file(‘radar_charts.svg‘)
结果如下图:
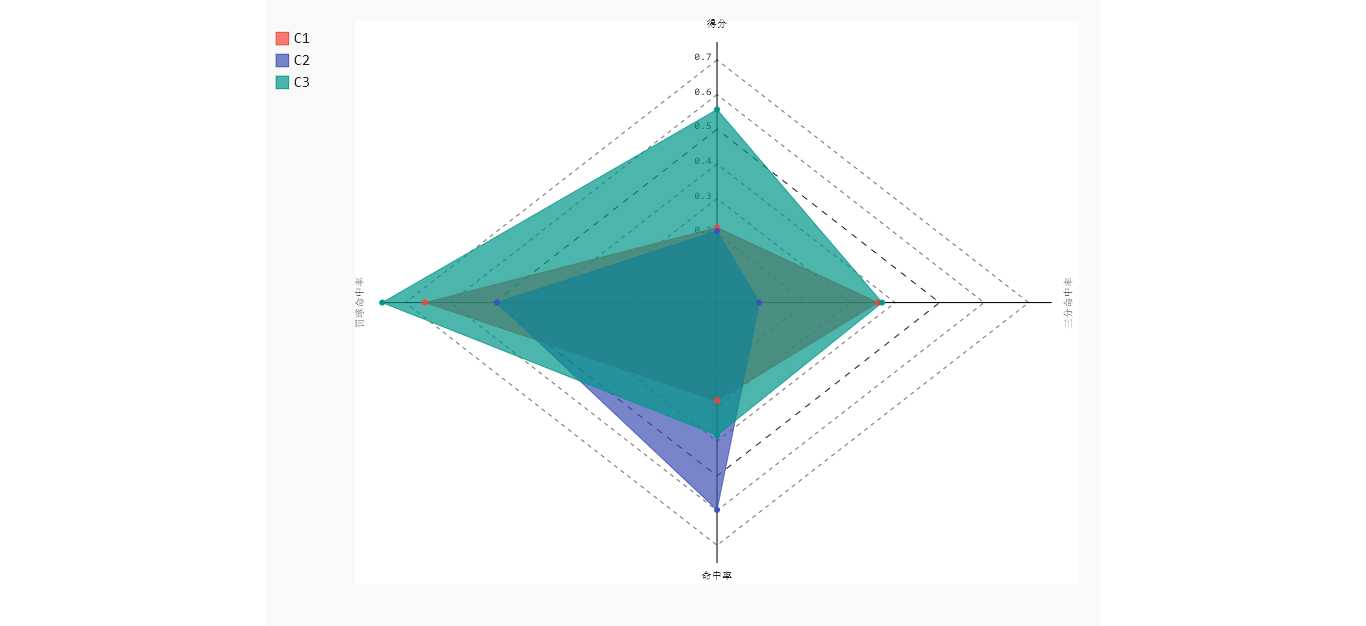
原文:https://www.cnblogs.com/hqczsh/p/11772243.html