太菜了 200pts
1.数据结构
题目描述
蒟蒻Edt把这个问题交给了你 ———— 一个精通数据结构的大犇,由于是第一题,这个题没那么难。。
edt 现在对于题目进行了如下的简化:
最开始的数组每个元素都是0
给出n,opt,min,max,mod,在int范围内
操作,
: ,, 表示把这个区间加上
(数组的从L到R的每个元素都加上X)
: , 表示询问这个区间中元素T满足 % 的 T这样的数的个数(i是数组下标)
(元素的值*数组下标%mod在min到max范围内)
由于 edt 请来了一位非三次元的仓鼠,他帮你用延后了部分问题,将这些询问打入了混乱时空,你的询问操作不会超过1000次,不幸的是,对于延后的询问操作可能有很多次(小于1e7次),但是保证这些延后的询问操作之后不会再次有修改操作
(就是在最后会有很多次询问,但不会进行修改)
解:
差分 我还以为我做的是暴力...
//
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#define maxnn 160100
#define ll long long
ll n,opt,mod,mi,ma,fi;
ll d[maxnn];
ll sum[maxnn];
#define GC getchar()
inline ll R() {
char t;
ll x=0;
t=GC;
ll f=1;
while(!isdigit(t)) {
if(t=='-') f=-1;
t=GC;
}
while(isdigit(t)) {
x=x*10+t-48;
t=GC;
}
return x*f;
}
void FIE(){
freopen("datastruct.in","r",stdin);
freopen("datastruct.out","w",stdout);
}
int main() {
//FIE();
char c;
n=R();
opt=R();
mod=R();
mi=R();
ma=R();
ll x,y,z;
while(opt--) {
c=getchar();
if(c=='A') {
x=R();
y=R();
z=R();
d[x]=(d[x]+z);
d[y+1]=(d[y+1]-z);
} else {
x=R();
y=R();
ll tot=0;
sum[0]=0;
ll tmp=0;
for(int i=1; i<=n; i++) {
tmp=(d[i]+tmp);
if((((tmp*i)%mod)>=mi)&&(((tmp*i)%mod)<=ma)) {
sum[i]=sum[i-1]+1;
} else {
sum[i]=sum[i-1];
}
}
printf("%lld\n",sum[y]-sum[x-1]);
}
}
ll tmp=0;
sum[0]=0;
for(int i=1; i<=n; i++) {
tmp=(d[i]+tmp);
if((((tmp*i)%mod)>=mi)&&(((tmp*i)%mod)<=ma)) {
sum[i]=sum[i-1]+1;
} else {
sum[i]=sum[i-1];
}
}
fi=R();
while(fi--) {
x=R();
y=R();
printf("%lld\n",sum[y]-sum[x-1]);
}
}2.答案错误
题目描述
每道WA了的题都会有一个分数,对于两个人的WA题程度是否相同,小X有这样一个评判方法:
无聊的她想了这样一个神奇的函数
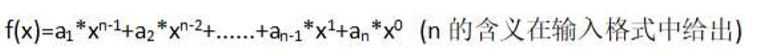
她认为,无论ai取什么值,两组f(x)的和都相等,则这两组题的错误程度很相似
假如有分值为 A={1,4,6,7 } ,B={2,3,5,8} 的两份被篡改完成的WA题,
问当n取一个数时 x的分组情况
说明
对于10%的数据,n<=4 , q<=10;
对于40%的数据,n<=20 , q<=5000;
对于100%的数据,n<=60 , q<=1000000;
解:
我还以为是秦九韶算法 原来是我想多了
首先分组情况一定唯一
数据范围很大 考虑打表
打一波n=5 时的表
根据暴力,我们有:
n=2时,A={1,4} , B={2,3};
n=3时,A={1,4,6,7} , B={2,3,5,8};
n=4时,A={1,4,6,7,10,11,13,16} , B={2,3,5,8,9,12,14,15}
是不是发现了什么
每次元素新增的是 \(2^(k-1)\) + 对面组的数
然后我们就可以暴力每次减去 2的次幂 然后判断操作的奇偶
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define maxnn 400000
LL n,k,x;
LL q;
LL A[maxnn];
int main()
{
cin>>n;
A[0]=1;
for(int i=1;i<=n;i++) A[i]=A[i-1]<<1;
cin>>q;
while(q--)
{
scanf("%lld",&x);
int k=0;
for(int i=n;i>=0;i--)
{
if(x>A[i]) {x-=A[i];k++;}
}
if(x==0)
{
if(k&1)
{
puts("X");
continue;
}
else
{
puts("Z");
continue;
}
}
else
{
if(k&1)
{
puts("Z");
continue;
}
else
{
puts("X");
continue;
}
}
}
}C3.部落冲突
限制 : 15000 MS - KB
评测说明 : 1s,128m
问题描述
clashclans.cpp/.in/.out
题目背景
在一个叫做Travian的世界里,生活着各个大大小小的部落。其中最为强大的是罗马、高卢和日耳曼。他们之间为了争夺资源和土地,进行了无数次的战斗。期间诞生了众多家喻户晓的英雄人物,也留下了许多可歌可泣的动人故事。
其中,在大大小小的部落之间,会有一些道路相连,这些道路是Travian世界里的重要枢纽,简单起见,你可以把这些部落与部落之间相连的道路看作一颗树,可见每条道路对于Travian世界的重要程度。有了这些道路,建筑工人就可以通过这些道路进行友好外交啦。
然而,事情并不会像想象的那样美好,由于资源的匮乏,相邻的部落(由一条道路相连的部落)之间经常会发生大大小小的冲突事件,更有甚者,会升级为部落之间的大型战争。
为了避免误伤,每当两个相邻的部落之间发生大型战争之时,这两个部落间的道路是不允许通行的,对于一些强大的部落,甚至能与多个相邻的部落同时开战,同样的,这些战争地带的道路十分危险,是不可通行的。
天下之势,分久必合,当两个部落经历了不打不相识的苦战之后,他们可以签订停战协议(暂时停战,以后依旧可能再次开战),这样,两个部落之间的道路又会重新恢复为可通行状态,建筑工人们又可以经过此地购买最新的大本营设计图纸来强大自己的部落了。
为了简单起见,我们把各大战争事件按发起的时间顺序依次编号(最先发起的战争编号就为 1,第二次战争编号就为 2,以此类推),当两个部落停战之时,则会直接告诉你这场战争的编号,然后这场战争就载入了史册,不复存在了,当然,这并不会影响到其他战争的编号。
建筑工人十分讨厌战争,因为战争,想从一个部落到另一个部落进行友好交流的建筑工人可能就此白跑一趟。所以,在他们出发之前,都会向你问问能不能到达他们想去的部落。
解:
树剖+树状数组
//
#include<bits/stdc++.h>
using namespace std;
#define maxnn 600000
#define lowbit(i) i&(-i)
int las[maxnn],en[maxnn],nex[maxnn],w[maxnn],tot;
int dep[maxnn],son[maxnn],size[maxnn];
int tr[maxnn],num;
int topp[maxnn];
int f[maxnn];
int dfn[maxnn],vii;
void add(int a,int b) {
en[++tot]=b;
nex[tot]=las[a];
las[a]=tot;
}
int c1[maxnn],c2[maxnn];
int n,m;
#define GC getchar()
inline int R() {
char t;
int x=0;
t=GC;
int f=1;
while(!isdigit(t)) {
if(t=='-') f=-1;
t=GC;
}
while(isdigit(t)) {
x=x*10+t-48;
t=GC;
}
return x*f;
}
void dfs1(int v,int fa) {
dep[v]=dep[fa]+1;
int maxson=-1;
size[v]=1;
f[v]=fa;
for(int i=las[v]; i; i=nex[i]) {
int u=en[i];
if(u!=fa) {
dfs1(u,v);
if(size[u]>maxson) {
son[v]=u;
maxson=size[u];
}
size[v]+=size[u];
}
}
}
void dfs2(int v,int fa,int to) {
dfn[v]=++vii;
topp[v]=to;
if(son[v]) {
dfs2(son[v],v,to);
}
for(int i=las[v]; i; i=nex[i]) {
int u=en[i];
if(u==fa) continue;
if(u==son[v]) continue;
{
dfs2(u,v,u);
}
}
}
void zad(int x,int d) {
for(int i=x; i<=n+100; i+=lowbit(i)) {
c1[i]+=d;
c2[i]+=x*d;
}
}
int get(int x) {
int ans=0;
for(int i=x; i; i-=lowbit(i)) {
ans+=(x+1)*c1[i];
ans-=c2[i];
}
return ans;
}
bool query(int x,int y) {
int ans=0;
while(topp[x]!=topp[y]) {
if(dep[topp[x]]<dep[topp[y]]) {
swap(x,y);
}
ans+=get(dfn[x])-get(dfn[topp[x]]-1);
if(ans) return false;
x=f[topp[x]];
}
if(dep[x]<dep[y]) {
swap(x,y);
}
ans+=get(dfn[x])-get(dfn[y]);
if(ans) return false;
return true;
}
void update(int x,int d) {
zad(dfn[x],d);
zad(dfn[x]+1,-d);
}
void FIE()
{
freopen("clashclans.in","r",stdin);
freopen("clashclans.out","w",stdout);
}
int main() {
//FIE();
int x,y;
n=R();
m=R();
for(int i=1; i<n; i++) {
x=R();
y=R();
add(x,y);
add(y,x);
}
dfs1(1,1);
dfs2(1,1,1);
char c;
while(m--) {
c=getchar();
while(c<'A'||c>'Z') c=GC;
if(c=='Q') {
x=R();
y=R();
if(query(x,y)) {
puts("Yes");
continue;
}
puts("No");
}
if(c=='C') {
x=R();
y=R();
if(dep[x]<dep[y]) {
swap(x,y);
}
tr[++num]=x;
update(x,1);
}
if(c=='U') {
x=R();
update(tr[x],-1);
}
}
}或者
如果没有修改操作就是从后往前然后利用bingchaji 判断连通性
注意到贡献到的是子树 所以考虑dfs序列
每次修改操作就修改子树的dfs序列的差分值 树状数组维护差分序列的前缀和
得到的就是到根的贡献 然后利用公式就行了
原文:https://www.cnblogs.com/OIEREDSION/p/11766085.html