


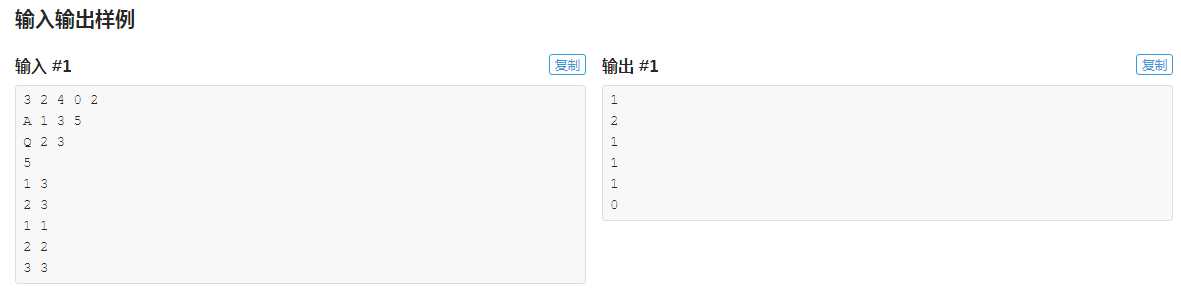
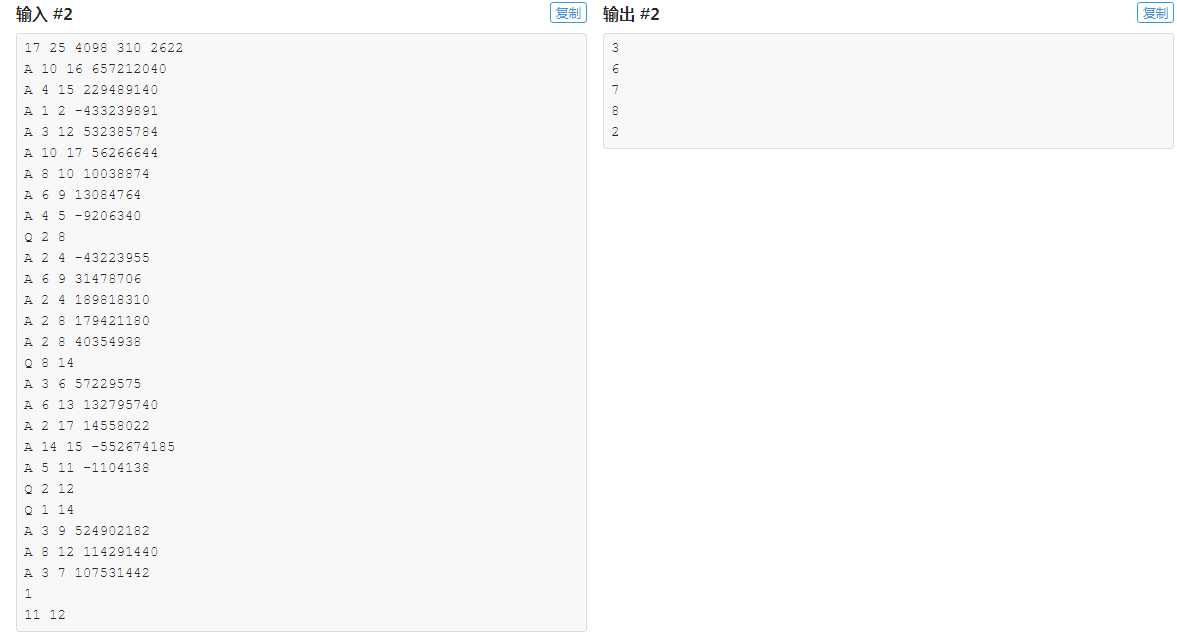
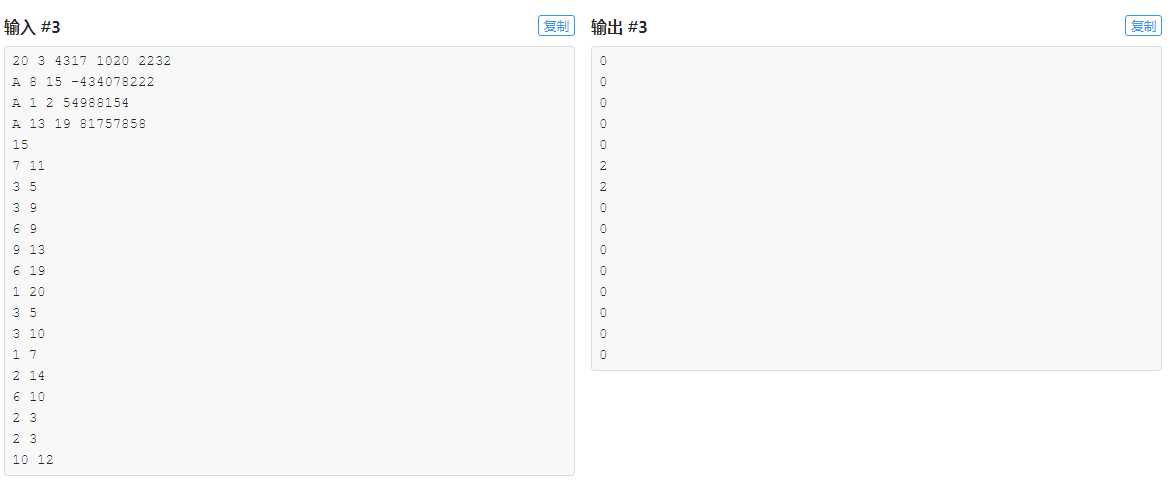

感觉这道题秀了我一地的智商。。。
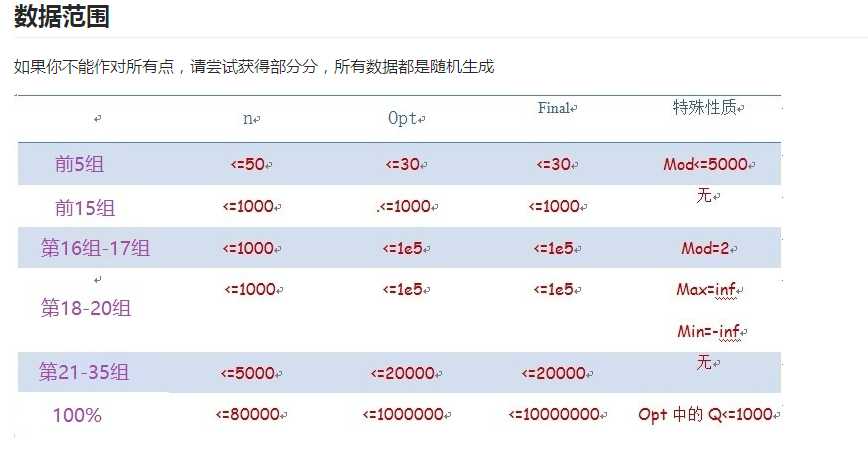
审题没审好,没确定带修改的操作中询问的次数<=1000,且max和min都是事先给好、不变的。想了半天线段树、分块,却忘了最基础的暴力。
写不出题时先写暴力。
先考虑在线的部分的做法:
因为修改的次数多,询问的次数少,而且询问很难在在线的情况下优化了,又发现数据随机,如果询问暴力处理的话最差复杂度也只有O(1000*n),在随机数据下复杂度远比此低。于是可以用差分优化区间加,询问暴力做就行。
离线部分:
显然不能暴力处理询问了,但是没有修改,又是区间询问个数,自然要想到前缀和优化了。设sum[i]为前i位满足条件的个数,扫一遍就能处理出sum,这是就能O(1)做询问了。
代码:
1 #include<iostream>
2 #include<cstdio>
3
4 using namespace std;
5
6 const int N=80005;
7
8 int n,opt,minn,maxx,fin,X;
9 int x,sum[N];
10
11 long long d[N],now,t,mod;
12
13 char ch;
14
15 bool f;
16
17 inline int read()
18 {
19 x=0;
20 f=0;
21 ch=getchar();
22 while(!isdigit(ch)) f|=(ch==‘-‘),ch=getchar();
23 while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
24 return f?-x:x;
25 }
26
27 inline char mygetchar()
28 {
29 ch=getchar();
30 while(ch!=‘A‘&&ch!=‘Q‘)
31 ch=getchar();
32 return ch;
33 }
34
35 void print(int a)
36 {
37 if(a>9)
38 print(a/10);
39 putchar(a%10+‘0‘);
40 }
41
42 int main()
43 {
44 // freopen("my.out","w",stdout);
45 n=read(),opt=read(),mod=read(),minn=read(),maxx=read();
46 char cao;
47 int l,r;
48 for(int i=1;i<=opt;++i)
49 {
50 cao=mygetchar();
51 if(cao==‘A‘)
52 {
53 l=read(),r=read(),X=read();
54 d[l]+=X;
55 d[r+1]-=X;
56 }
57 else
58 {
59 l=read(),r=read();
60 int ans=0,j;
61 now=0;
62 for(j=1;j<l;++j)
63 now+=d[j];
64 for(j=l;j<=r;++j)
65 {
66 now+=d[j];
67 t=now%mod*j%mod;
68 if(t>=minn&&t<=maxx)
69 ans++;
70 }
71 print(ans);
72 putchar(‘\n‘);
73 }
74 }
75 fin=read();
76 now=0;
77 for(int i=1;i<=n;++i)
78 {
79 now+=d[i];
80 t=now%mod*i%mod;
81 sum[i]=sum[i-1]+(t>=minn&t<=maxx);
82 }
83 for(int i=1;i<=fin;++i)
84 {
85 l=read(),r=read();
86 print(sum[r]-sum[l-1]);
87 putchar(‘\n‘);
88 }
89 return 0;
90 }
总结:写不出题想想暴力(没准就是正解呢)
差分多用于优化离线的区间修改。
前缀和多用于离线的区间查询。
原文:https://www.cnblogs.com/InductiveSorting-QYF/p/11766051.html