数据类型

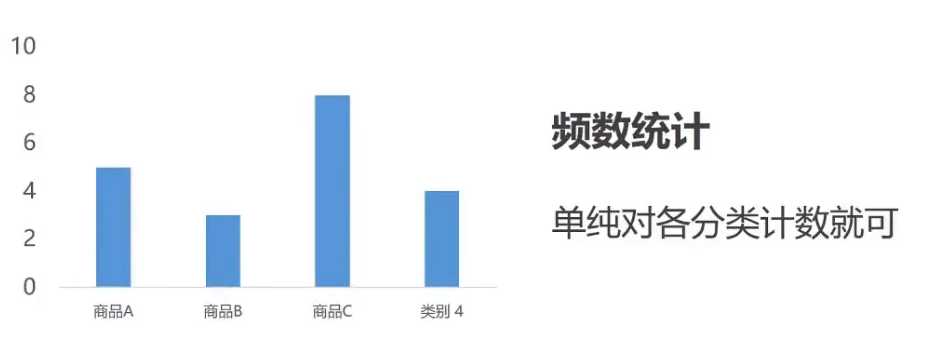
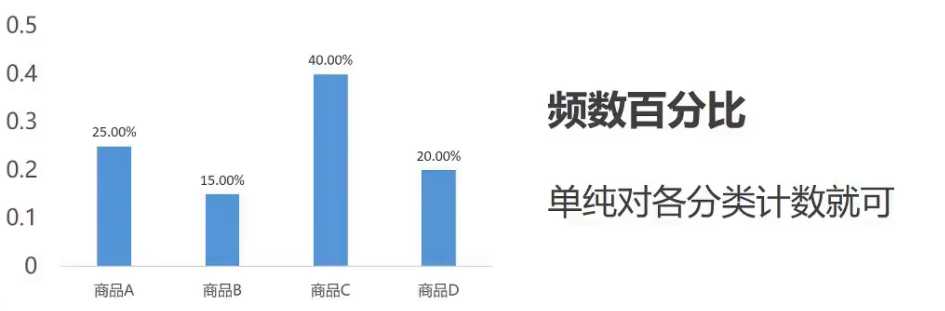
数据数据一般是可以直接加载运算的数据， 一般是整形浮点型等

分类数据则为文本数据， 比如男女， 雌雄等

分类数据描述统计

数值数据描述统计

平均数， 中位数， 众数

平均数 - 求和均分 - 较为适合再数据平稳的样本中

中位数 - 最中间的数值 - 目的查看最中间的数据

众数 - 最多的数值 - 目的查看构成最多的数据

平均数和中位数可以联动分析

　　平均数比中位数大的话说明 极大数据量或者较大数据量比较集中， 数据向上偏移

　　平均数比中位数小的话说明 极小数据量或者较小数据量比较集中， 数据向下偏移

中位数

中位数可以四等分， 10等分， 百等分等等

最中间的中位数就是普通的中位数

方差， 标准差

 用于描述数值的离散程度， 公式计算如下

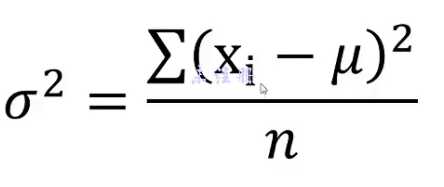
方差的单位是平方 因此这里引入标准差， 对方差开根号， 从而可以得出的现实意义是

大部分的数据波动再 平均值附近 +- 标准查的上下限， 从而得出一个理论上的阈值

描述上更喜欢用标准查来更好的贴合业务

数据标准化 Z-Score

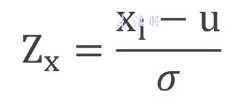
x_i 每组数据的具体值， u 平均值， σ 标准差。 Z_x 标准化后的结果

不同数量级不同纬度的数据是没办法一起对比的

因此需要对数据进行统一格式， 或者压缩格式标准化处理

标准化后的数值会在 0-1 之间上下波动， 从而反应原始数据的一个特征

权重预估

数据标准化时可以加入权重， 

比如 （3 x a + 2 x b + 1 x c ）/ 6 这样计算则是对 a 给与了3 的权重，表示更重视 a 的数据

切比雪夫定理

示例

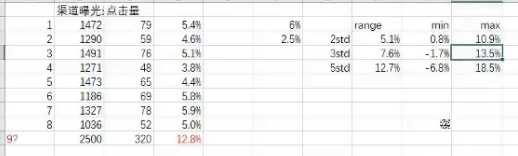
 第9 渠道的点击率达到 12. 远远大于其他怎么判断9渠道是否是异常还是正常？

根据切比雪夫定理， 计算出的标准查为 2.5 ， 平均点击率 是 6 

两个偏差的 区间是  0.8 - 10.9 

三个偏差的 区间是  0 - 13.5

五个偏差的 区间是 0 - 18.5 

现实意义的 点击率是不能为 负数 ， 因此左节点为 0

这样比对， 12.8 再 三个偏差的范围

即， 发生此现象的可能性是 11% 

excel 相关的函数

平均数 　　 =AVG

中位数  　　=MEDIAN

众数 　　 =MODE

分位数 　　=QUARTILE

方差 　　 = VAR_P

标准差 　　=STDEV

综合 -  数据 - 数据分析 - 汇总统计

数值数据描述统计可视化

箱线图

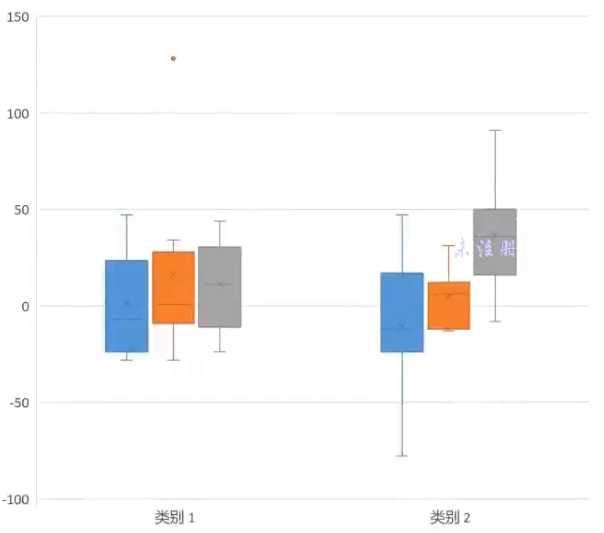
通过箱体可以简单的判断大部分的中间数据再哪里， 这部分的数据是再 25-75 之间的数据

图形中的 x 表示的是平均数， 平均数和中位线的对比可以得知样本数据的整体偏差

 IQR 表示的是 第三分位数 - 第一分位数， 从而可以推出上下边缘

上下边缘偏向于经验推算， 表示大部分的数据都会再此区间囊括

对于大于上小于下之类的点则作为异常数据看待

直方图

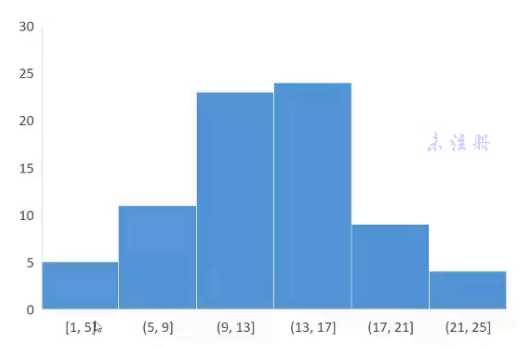
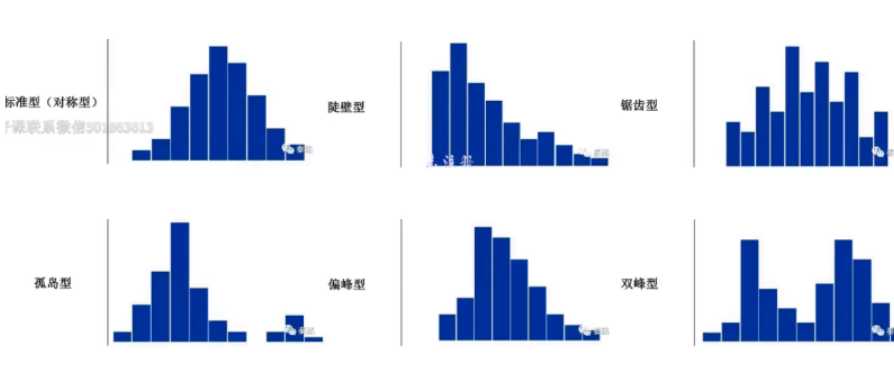
直方图一般是等距划分， 而且下面的划分， 数值点的判定是不能重叠， 

是以 开闭区间一起对应这样保证唯一

常见得图形

数据分析 - 基础理论 - 描述统计学

原文：https://www.cnblogs.com/shijieli/p/11733671.html