http://poj.org/problem?id=2349
Description
国防部(DND)要用无线网络连接北部几个哨所。两种不同的通信技术被用于建立网络:每一个哨所有一个无线电收发器,一些哨所将有一个卫星频道。
任何两个有卫星信道的哨所可以通过卫星进行通信,而不管他们的位置。同时,当两个哨所之间的距离不超过D时可以通过无线电通讯,D取决于对收发器的功率。功率越大,D也越大,但成本更高。出于采购和维修的方便,所有哨所的收发器必须是相同的;那就是说,D值对每一个哨所相同。
你的任务是确定收发器的D的最小值。每对哨所间至少要有一条通信线路(直接或间接)。Input
输入的第一行是测试数据的数量N。
每组测试数据的第一行包含卫星频道的数量S(1 < = S < = 100)和哨所的数量P(S < P < = 500)。接下来的P行,给出以公里为单位的每个哨所的坐标(x,y)( 坐标为0到10000之间的整数)。Output
对于每组测试数据,输出一行,输出收发器的D的最小值。精确到小数点后两位。
1 2 4 0 100 0 300 0 600 150 750
212.13
题意:
有P个地方,它们之间的联系方式有2种,卫星和无线电。有卫星的地方就不需要无线电了,题目输入P个地方的坐标,其中S个地方有卫星装置,没有卫星装置的只能用无线电,要使这些地方之间能通信,问最优情况下的最大无线电长度。
思路:
把P个点连接成一个最小生成树,去掉最大的S-1个长度,再求剩下最小生成树中树枝最长的长度
证明来自:https://blog.csdn.net/mengxiang000000/article/details/51482790
1、因为我们是按照剩余建造的边中最大值作为D的值来输出,那么我们一定是尽量的让D小,也就是说在入树的边中选取最大边让他尽可能小,才是我们要的结果,既然是这样,我们应该尽量将这s个城市,建造出来之后,让一些树中的边权尽可能大的边不许要建造即可。
2、至于我们要拆除的边,我们已经明确了:尽量让其边权值更大,那么我们s个城市如何分配呢?首先我们先这样来处理,使用两个点,来使得树中最大权值边不需要建造了,我们不妨拿出例子:
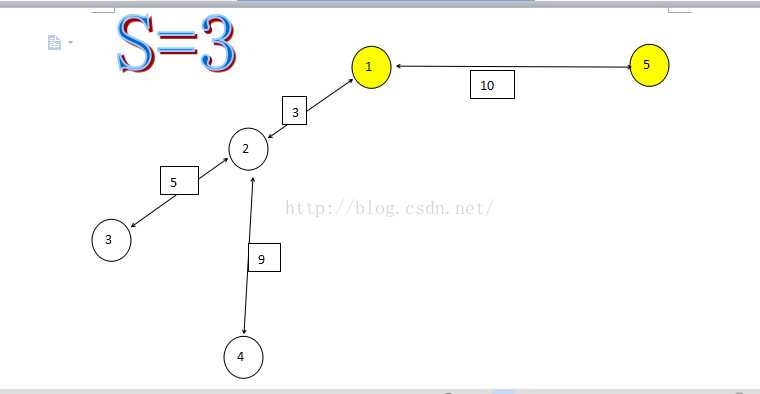
按照刚刚情况来看,我们选取节点1、5来使得权值为10的边不需要建造,因为这个时候S=3,所以我们还有一个点可以选,这个时候我们想要贪心的使得9这条边不需要建造,这个时候D就可以等于5了,是最理想的状态,那么是不是去掉权值为9这条边也是一定需要两个点来搞定呢?明显不需要,这个时候我们再选取一下节点4 ,使得1、2、5三个节点都相互连通了,相当于我们的图变成只有1、2、3三个节点所构成的树了,这个时候我们取得最大权值边就是D的值,为5。也就是说,有s个点,就一定能够去掉S-1条边,这个时候我们直接贪心去边即可。
代码如下:
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 //const double PI=acos(-1); 17 #define Bug cout<<"---------------------"<<endl 18 const int maxn=1e4+10; 19 using namespace std; 20 21 struct edge_node 22 { 23 int to; 24 double val; 25 int next; 26 }Edge[maxn*maxn/2]; 27 int Head[maxn]; 28 int tot; 29 30 struct point_node 31 { 32 double x; 33 double y; 34 }PT[maxn]; 35 36 37 void Add_Edge(int u,int v,double w) 38 { 39 Edge[tot].to=v; 40 Edge[tot].val=w; 41 Edge[tot].next=Head[u]; 42 Head[u]=tot++; 43 } 44 45 double lowval[maxn]; 46 int pre[maxn];//记录每个点的双亲是谁 47 double ans[maxn];//存放最小生成树的权值 48 int ans_cnt;//ans数组计数器 49 50 double Prim(int n,int m,int st)//n为顶点的个数,st为最小生成树的开始顶点 51 { 52 ans_cnt=0; 53 fill(lowval,lowval+n,INF);//不能用memset(lowval,INF,sizeof(lowval)) 54 memset(pre,0,sizeof(pre)); 55 lowval[st]=-1; 56 pre[st]=-1; 57 for(int i=Head[st];i!=-1;i=Edge[i].next) 58 { 59 int v=Edge[i].to; 60 double w=Edge[i].val; 61 lowval[v]=min(lowval[v],w); 62 pre[v]=st; 63 } 64 for(int i=0;i<n-1;i++) 65 { 66 double MIN=INF; 67 int k; 68 for(int i=0;i<n;i++)//根据编号从0或是1开始,改i从0--n-1和1--n 69 { 70 if(lowval[i]!=-1&&lowval[i]<MIN) 71 { 72 MIN=lowval[i]; 73 k=i; 74 } 75 } 76 ans[ans_cnt++]=MIN; 77 lowval[k]=-1; 78 for(int j=Head[k];j!=-1;j=Edge[j].next) 79 { 80 int v=Edge[j].to; 81 double w=Edge[j].val; 82 if(w<lowval[v]) 83 { 84 lowval[v]=w; 85 pre[v]=k; 86 } 87 } 88 } 89 double ANS=0; 90 sort(ans,ans+ans_cnt); 91 for(int i=0;i<ans_cnt-(m-1);i++) 92 if(ans[i]>ANS) 93 ANS=ans[i]; 94 return ANS; 95 } 96 97 int main() 98 { 99 int T; 100 scanf("%d",&T); 101 while(T--) 102 { 103 int n,m; 104 scanf("%d %d",&m,&n); 105 memset(Head,-1,sizeof(Head)); 106 tot=0; 107 for(int i=0;i<n;i++) 108 { 109 scanf("%lf %lf",&PT[i].x,&PT[i].y); 110 } 111 for(int i=0;i<n;i++) 112 { 113 for(int j=i+1;j<n;j++) 114 { 115 double x,y; 116 x=PT[i].x-PT[j].x; 117 y=PT[i].y-PT[j].y; 118 double val=sqrt(x*x+y*y); 119 Add_Edge(i,j,val); 120 Add_Edge(j,i,val); 121 } 122 } 123 printf("%.2f\n",Prim(n,m,0)); 124 } 125 return 0; 126 }
POJ-2349 Arctic Network(最小生成树+减免路径)
原文:https://www.cnblogs.com/jiamian/p/11731810.html