在Bagging策略的基础上进行修改后的一种算法:
Extra Tree是RF的一个变种,原理基本和RF一样,区别如下 :
Extra Tree因为是随机选择特征值的划分点,这样会导致决策树的规模一般大于RF所生成的决策树,也就是说Extra Tree模型的方差相对于RF进一步减少;在某些情况下,Extra Tree的泛化能力比RF的强。
IForest是一种异常点检测算法,使用类似RF的方式来检测异常点;IForest算法和RF算法的区别在于:
区别原因:IForest的目的是进行异常点检测,因此只要能够区分异常点即可,不需要大量数据;另外在异常点检测过程中,一般不需要太大规模的决策树
计算方式:
\[ p(x,m)=2^{-\frac{h(x)}{c(m)}} \]
\[ c(m)=2ln (m-1)+\xi-2\frac{m-1}{m};m-为样本个数,\xi-欧拉常数 \]
Boosting(提高)指的是:通过算法集合,将弱学习器转换为强学习器。
Boosting每一步产生弱预测模型(如决策树),并加权累加到总模型中;
Boosting的意义:如果一个问题存在弱预测模型,那么可以通过提升技术的办法得到一个强预测模型;
常见的Boosting算法有:
boosting算法的工作机制:
如下图所示:
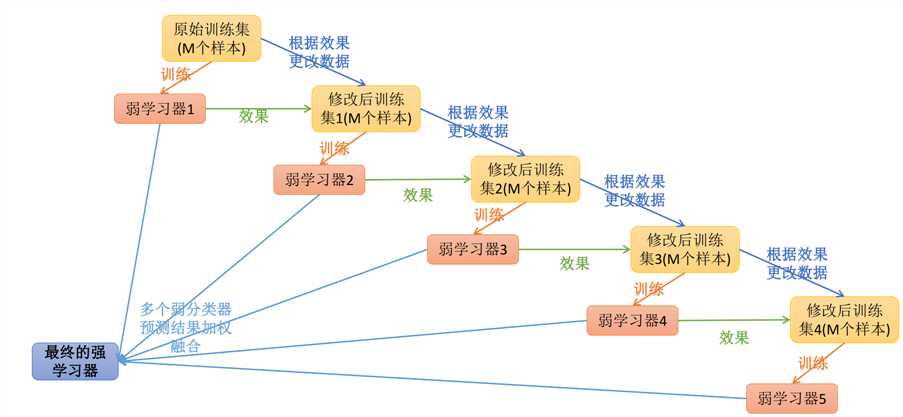
Adaptive Boosting是一种迭代算法。
每轮迭代中会在训练集上产生一个新的学习器,然后使用该学习器对所有样本进行预测,以评估每个样本的重要性(Informative)。换句话来讲就是,算法会为每个样本赋予一个权重,每次用训练好的学习器标注/预测各个样本,如果某个样本点被预测的越正确,则将其权重降低;否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大,也就是说越难区分的样本在训练过程中会变得越重要;
整个迭代过程直到错误率足够小或者达到一定的迭代次数为止
Adaptive Boosting算法将基分类器的线性组合作为强分类器,同时给分类误差率较小的基本分类器以大的权值,给分类误差率较大的基分类器以小的权重值;构建的线性组合为:
\[
f(x)=\sum_{m=1}^{M}{\alpha_mG_m(x)}
\]
最终强学习器是在线性组合的基础上进行Sign函数转换:
\[
G(x)=sign(f(x))=sign[\sum_{m=1}^{M}{\alpha_mG_m(x)}]
\]
其损失函数为:
\[
loss=\frac{1}{n}\sum_{i=1}^{n}{I(G(x_i) \neq y_i)}
\]
由函数的关系可得,该损失函数有上界:
\[
loss=\frac{1}{n}\sum_{i=1}^{n}{I(G(x_i) \neq y_i)} \leq \frac{1}{n}\sum_{i=1}^{n}{e^{-y_if(x)}}
\]
计算第K-1轮和k轮的学习器分别为:
\[
f_{k-1}(x)=\sum_{j=1}^{k-1}{\alpha_jG_j(x)}
\]
\[ f_{k}(x)=\sum_{j=1}^{k-1}{\alpha_jG_j(x)}=f_{k-1}(x)+\alpha_kG_k(x) \]
损失函数如下:
\[
loss(\alpha_m,G_m(x))=\frac{1}{n}\sum_{i=1}^{n}{e^{-y_if(x)}}=\frac{1}{n}\sum_{i=1}^{n}{e^{-y_i(f_{k-1}(x)+\alpha_kG_k(x))}}
\]
\[ =\frac{1}{n}\sum_{i=1}^{n}{e^{-y_if_{k-1}(x)}e^{-y_i\alpha_kG_k(x)}} \]
由于其中\(e^{-y_if_{k-1}(x)\)的值在K轮前已经求得,因此令该值为\(\omega_{mi}\),经过变换后,上式为:
\[
=\frac{1}{n}\sum_{i=1}^{n}{\omega_{mi} e^{-y_i\alpha_kG_k(x)}}
\]
因此使上式达到最小的\(\alpha_m\)和\(G_m\)就是AdaBoost算法的最终求解值。
G这个分类器在训练过程中,是为了让误差率最小,所以可以认为G越小其实就是误差率越小
\[ G_m^*(x)=\frac{1}{n}\sum_{i=1}^{n}{\omega_{mi}I(y_i\neq G_m(x_i))} \]\[ \varepsilon=P(G_m(x)\neq y)=\frac{1}{n}\sum_{i=1}^{n}{\omega_{mi}I(y_i\neq G_m(x_i))} \]
对于\(\alpha_m\)而言,通过求导然后令导数为0,可得公式:
\[ \alpha_m^*=\frac{1}{2}ln {(\frac{1-\varepsilon_m}{\varepsilon_m})} \]
\[ T={(x_1,y_1), (x_2,y_2),...,(x_n,y_n)} \]
\[ D_1=(w_{11},w_{12},...,w_{1i},...,w_{1n}),w_{1i}=\frac{1}{n},i=1,2,...,n \]
\[ G_m(x):x取-1或1 \]
\[ \varepsilon_m=\sum_{i=1}^{n}P(G_m(x_i)\neq y_i)=\sum_{i=1}^{n}{\omega_{mi}I(y_i\neq G_m(x_i))} \]
\[ \alpha_m^*=\frac{1}{2}ln {(\frac{1-\varepsilon_m}{\varepsilon_m})} \]
\[ D_{m+1}=(w_{m+1,1}, w_{m+1,2}, ...,w_{m+1,n}) \]
\[ 其中:w_{m+1,i}=\frac{w_{m,i}}{Z_m}e^{-\alpha_my_iG_m(x_i)} \]
\[ 其其中:Z_m=\sum_{i=1}^{n}{e^{-\alpha_my_iG_m(x_i)}} \]
\[ f(x)=\sum_{m=1}^{M}{\alpha_mG_m(x)} \]
\[ G(x)=sign(f(x))=sign[\sum_{m=1}^{M}{\alpha_mG_m(x)}] \]
GBDT(Gradient Boosting Decision Tree),也是Boosting算法中的一种,和Adaboost的区别如下:
\[ 初始时:f_{t-1}(x),Loss(y,f_{t-1}(x)) \]
\[ 经过训练:f_{t}(x),Loss(y,f_{t-1}(x)+h_t(x)) \]
直观理解上:
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,在第一次预测结果为20岁,发现损失为10岁,这次我们预测结果为6岁,发现差距还有4岁,第三轮预测结果为3岁去拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小
GBDT由三部分构成:
DT(Regression Decistion Tree):由多棵决策树构成,所有树的结果累加起来就是最终结果
和随机森林区别如下:
随机森林的子树之间是没有关系的;而GBDT在构建子树时,使用的是之前子树构建结果后形成的残差作为输入数据,因此子树之间是有关系的
GB(Gradient Boosting)
Shrinking
\[ L(Y, F(X))=\frac{1}{2}(Y-F(X)^2),L(Y, F(X))=|Y-F(X| \]
\[ F^*(X)=argmin_FL(Y, F(X)) \]
\[ 其中F(X)为一组最优基函数f_i(X)的加权和 \]
\[ F(X)=\sum_{i=0}^{T}{f_i(X)} \]
\[ 防止每个学习器能力过强,可能导致过拟合,可给定一个缩放系数v \]
\[ F(X)=v\sum_{i=0}^{T}{f_i(X)} \]
\[ F_t(X)=F_{t-1}(X)+argmin_f\sum_{i=1}^{m}{L(y_i, F_{t-1}(x_i)+f_t(x_i))} \]
\[ argmin_f\sum_{i=1}^{m}{L(y_i, F_{t-1}(x_i)+f_t(x_i))} \]
\[ 当使用MSE时:argmin_f\sum_{i=1}^{m}{\frac{1}{2}(y_i-F_{t-1}(x_i)-f_t(x_i))^2} \]
\[ 第t轮第i个样本的损失函数的负梯度为:-[\frac{?L(y_i,F(x_i))}{?F(x_i)}]_{F(x_i)=F_{t-1}(x_i)} \]
\[ =y_i-F(x_i),令其为\alpha_{ti} \]
有如下发现,损失函数的一阶负梯度的值正好等于残差
\[ \alpha_{tj}=argmin_c\sum_{x_i∈R_{tj}}{L(y_i,F_{t-1}(x_i)+c)} \]
\[ h_t(x)=\sum_{j=1}^{J}{c_{tj}I(x∈R_{tj})} \]
\[ F_t(x)=F_{t-1}(x)+\sum_{j=1}^{J}{c_{tj}I(x∈R_{tj})} \]
对于上述流程理解的还不是十分的透彻,部分内容摘录自一下博文中:
两者唯一的区别就是选择了不同的损失函数
在回归算法中,一般选择均方差作为损失函数;在分类算法中一般选择对数函数作为损失函数
\[ L(y,f(x))=ln (1+e^{-y \times f(x)}),y取-1/1 \]
\[ L(y,f(x))=-\sum_{k=1}^{K}{y_klog(p_k(x))} \]
Bagging和Boosting的区别:
- 样本选择:Bagging是有放回的随机采样;Boosting是采用所有的训练样本,只是在迭代过程中更改样本的权重信息;
- 预测函数:Bagging所有预测模型的权重相等;Boosting对于误差小的模型有更大的权重;
- 并行计算:Bagging可以通过并行生成各个模型;Boosting由于下一个模型依赖于上一个模型,因此只能顺序产生;
- 方差偏差:Bagging减少了模型的方差(variance);Boosting减少了模型的偏差(bias)
参考知乎上大牛的解释:https://www.zhihu.com/question/26760839/answer/40337791
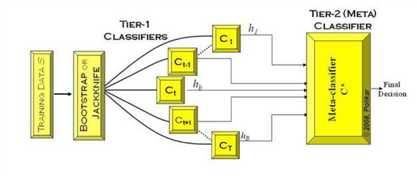
Stacking是指训练一个模型用于组合(combine)其它模型(基模型/基学习器)的技术。即首先训练出多个不同的模型,然后再以之前训练的各个模型的输出作为输入来新训练一个新的模型,从而得到一个最终的模型。一般情况下使用单层的Logistic回归作为组合模型,其大致结构如下图所示:
GitHub:
https://github.com/zhuChengChao/ML-Ensemble
原文:https://www.cnblogs.com/zhuchengchao/p/11731838.html