算法第三章上机实践报告

1、实践题目：

7-1 数字三角形

给定一个由 n行数字组成的数字三角形如下图所示。试设计一个算法，计算出从三角形 的顶至底的一条路径(每一步可沿左斜线向下或右斜线向下)，使该路径经过的数字总和最大。

输入格式:

输入有n+1行：

第 1 行是数字三角形的行数 n，1<=n<=100。

接下来 n行是数字三角形各行中的数字。所有数字在0..99 之间。

输出格式:

输出最大路径的值。

输入样例:

在这里给出一组输入。例如：

5 
7 
3 8 
8 1 0 
2 7 4 4
4 5 2 6 5 

输出样例:

在这里给出相应的输出。例如：

30

2、问题描述：

根据题干所给的一个三角形，即二维数组的下三角形，求出从顶部到底部最佳的路线，使得经过的数字总和最大。

3、算法描述

易知该问题应使用动态规划的方法，存在重叠子问题。

首先思考递归方程以及如何记录最大数字总和：

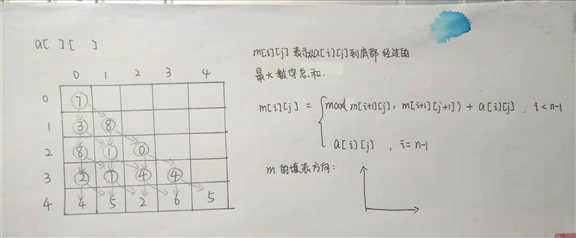
 然后思考如何用代码实现：

#include<iostream>
using namespace std;

int Max(int a, int b){
	return (a > b) ? a : b;
}

int main(){
	int a[101][101];
	int m[101][101]; 
	int n;
	cin >> n;
	int max;
	for(int i=0; i<n; i++){
		for(int j=0; j<=i; j++){
			cin >> a[i][j];
		}
	}
	
	for(int j=0; j<n; j++){
		m[n-1][j] = a[n-1][j];
	}
	
	for(int i=n-2; i>=0; i--){
		for(int j=0; j<n; j++){
			m[i][j] = Max(m[i+1][j], m[i+1][j+1]) + a[i][j];
		}
	}
	max = m[0][0];
	cout << max;
	return 0;
} 

4、算法时间及空间复杂度分析（要有分析过程）

时间复杂度：初始化数组使用for循环嵌套，时间复杂度为O（n²),填表也使用了for循环嵌套，时间复杂度为O（n²),所以整个算法的时间复杂度为O（n²)。

空间复杂度：因为需要用到辅助空间二维数组进行填表，所以空间复杂度是O（n²)。

5、心得体会（对本次实践收获及疑惑进行总结）

• 对于动态规划有了更为深入的理解，不再只停留于理论，开始有点学会如何用这种方法来解决问题（虽然还是很困难，不能完全脱离书本）；
• 对于我来说，解决该问题的难点在如何建立递归方程以及如何记录已经解决的子问题。我们一开始是定义了一个函数来想要解决问题，但是该函数需要将二维数组作为参数传给它，我们一开始不知道错在哪里，于是将它放进主函数里。课后查找我才发现二维数组传参，必须事先规定列数，这让我明白知识是层层递进的，我们一定要打好基础。
• 相比于上一次合作，这一次我和小伙伴的合作更加融洽，更加有默契，解决问题的速度也得到了一定的提高。

算法第三章上机实践报告

原文：https://www.cnblogs.com/WWYlaowu/p/11706376.html