

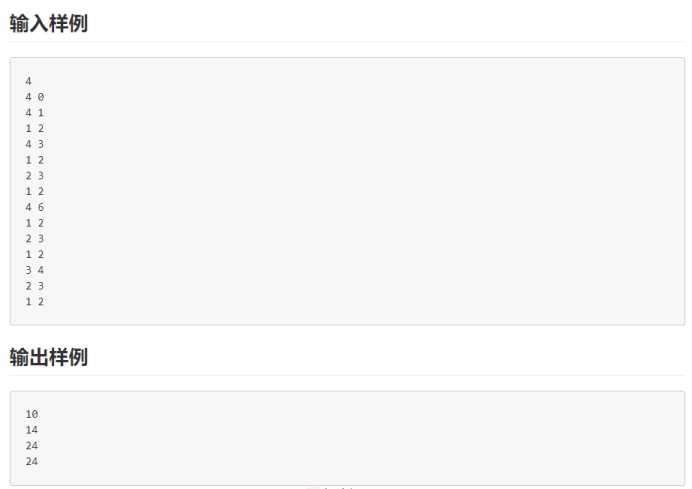
针对这个问题,首先可以想到有两种解决方法:构造全排列然后分别筛选后进行判断,逆序判断。
而显然对于前者时间是一定不够的(10以上数字的全排列构建时间就已经很长了),所以需要进行逆序判断。
即如果是符合条件的数组,那么经过筛选器后一定会是一个即将排好序的数组。所以只需要对所有即将排好序的数组倒序通过筛选器,得到筛选前的数组再判断即可。
注意筛选器的处理有两种可能:不必更换和更换两个位置的值,所以在判断之前的筛选器时需要分别对更换前后进行判断。
而对于即将排好序的数组的构建,可以使用巧妙方法:先1-n分别放在对角线处,然后将剩下的值按顺序放入空白的地方,就一定是一个即将排好序的数组(注意进行重复数组的去除)。
这里也是只语言描述不够清晰,还是参考代码进行最好。
#include<iostream>
using namespace std;
int num[100000][51];
int filter[11][2];
long long ans = 0;
void dfs(int t,int a[]){
int temp;
if (t == 0) {//经过了所有筛选器筛选,所以++
ans++;
return ;
}
int l = filter[t][0];
int r = filter[t][1];
if (a[l] > a[r])//不可能是经过这个筛选器得到的数列,所以直接返回
{
return ;
}
else
{
//判断前一个筛选器
dfs(t-1,a);
//交换后再进行判断
temp = a[l];
a[l] = a[r];
a[r] = temp;
dfs(t-1,a);
//交换回来防止出错
temp = a[r];
a[r] = a[l];
a[l] = temp;
}
}
int main()
{
int cnt,fcnt;
int n,N;
int i,j;
cin >> cnt;
while(cnt--)
{
ans = 0;
cin >> n >> fcnt;
N = n*n;
for (i=1;i<=fcnt;i++)
{
cin >> filter[i][0] >> filter[i][1];
}
//准备构建即将排好序的数列,把1-n分别放到对角线
for (i=1;i<=n;i++)
{
for (j=1;j<=n;j++)
{
num[(i-1)*n+j][j] = i;//(i-1)*n+j就是自动随着j向下移动
}
}
//补充空白的位置,按顺序把剩下的填进去
for (i=1;i<=n;i++)
{
for (j=1;j<=n;j++)
{
for (int k=1,temp=1;k<=n;k++)
{
if (temp==i) temp++;//是填入的值所以跳过
if (k==j) continue;//已经有之前填入的对角线了
num[(i-1)*n+j][k] = temp++;
}
}
}
//将重复的数列进行屏蔽处理
for (i=1;i<=N;i++){
for (j=i+1;j<=N;j++){
//遍历判断是否相同
int k = 1;
for(;num[j][k]==num[i][k]&&k<=n;k++){}
if(k==n+1) num[j][1] = -1;
}
}
//分别对即将排好序的数列进行反向筛选
for (i=1;i<=N;i++){
if (num[i][1] == -1) continue;
dfs(fcnt,num[i]);
}
cout << ans << endl;
}
return 0;
}
原文:https://www.cnblogs.com/doUlikewyx/p/11701188.html