线性表的定义

　　由 n (n≥0) 个数据元素 (a_1, a₂, ..., a_n) 构成的有限序列。记作：L =  (a_1, a₂, ..., a_n) 。a₁——首元素，a_n——尾元素。

　　表的长度（表长）——线性表中数据元素的数目。

　　空表——不含数据元素的线性表（表长为0）。

线性表的特征

　　对于L =  (a_1, a₂, ...,a_i-1, a_i ,a_i+1, ..., a_n)

1. 1. a_i-1 在 a_i 之前，称a_i-1 是 a_i 的直接前驱（1<i≤n）;
   2. a_i+1 在 a_i 之后，称a_i+1 是 a_i 的直接后继（1≤i<n）;
   3. a₁ 没有前驱；
   4. an 没有后继；
   5. a_i (1<i<n)有且仅有一个直接前驱和一个直接后继。

抽象数据类型线性表的定义

　　ADT List

　　{　　数据对象：D = { a_i | a_i∈ElemSet，i = 1, 2, ..., n, n>=0 }

　　　　 数据关系：R1 = { <a_i-1, a_i > | a_i-1, a_i∈D, i = 1, 2, ..., n }

　　　　 基本操作：

1. 1. 1. InitList (&L) 　　//构造空表L
      2. ListLength (L)　　//求表的长度
      3. GetElem (L, i, &e)　　//取元素 a_i ，由 e 返回 a_i
      4. PriorElem (L, ce, &pre_e)　　//求 ce 的前驱，由 pre_e 返回
      5. InsertElem (&L, i, e)　　//在元素 a_i 之前插入新元素 e
      6. DeleteElem (&L, i)　　//删除第 i 个元素
      7. EmptyList (L)　　//判断是否为空表

　　　　　　　　　　......

　　} ADT List

　　说明：

1. 删除表 L 中第 i 个数据元素 (1<=i<=n)，记作：DeleteElem (&L, i)；指定序号，删除a_i
2. 指定元素值 x ，删除表 L 中的值为 x 的元素，记作：DeleteElem (&L, x)；若 a_i = x，删除a_i
3. 在元素 a_i 之前插入新元素 e (1<=i<=n+1)，记作：InsertElem (&L, i, e)
4. 查找——确定元素值（或数据项的值）为 e 的元素。若有一个 a_i = e，则称“查找成功”(i = 1, 2, ... , n)
5. 排序——按元素值或某个数据项值的递增（或递减）次序重新排列表中各元素的位置
6. 将表 La 和 Lb 合并为 Lc
7. 表 La 复制为表 Lb 

线性表的顺序表示

　　顺序分配： (a_1, a₂, ..., a_n)  顺序存储结构的一般形式

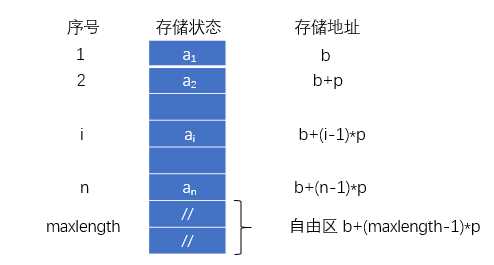
　　b 表示表的首/基地址

　　p 表示1个数据元素所占存储单元的数目

　　例1：分别定义元素所占空间、表长、尾元素的位置

#define maxleng 100
{
    ElemType la[maxleng+1];
    int length;    //当前长度
    int last;    //an的位置
}

静态分配

　　例2：元素所占空间和表长合并为C语言的一个结构类型：

#define maxleng 100
typedef struct
{
    ElemType elem[maxleng];
    int length;    //表长
} Sqlist;
Sqlist La;

　　其中：typedef——别名定义，Sqlist——结构类型名，La——结构类型变量名，La.length——表长，La.elem[0]——a₁，La[La.length-1]——a_n

动态分配

#define LIST_INIT_SIZE 100
#define LISTINCREMENT 100
typedef struct
{
    ElemType *elem;    //存储空间基地址
    int length;
    int listsize;    //当前分配的存储容量 以 sizeof(ElemType)为单位
} Sqlist;
Sqlist Lb;

寻址公式

　　假设：线性表的首地址为 b，每个数据元素占 p 个存储单元，则表中任意元素  (1<=i<=n)的存储地址是：LOC(i) = LOC(1) + (i - 1) * p = b + (i - 1) * p，(1<=i<=n)

顺序表的插入算法

　　在线性表L =  (a_1, a₂, ...,a_i-1, a_i ,a_i+1, ..., a_n)中的第 i 个元素前插入元素 x 

　　移动元素下标范围：i - 1 ~ n - 1 或 i - 1 ~ L.length - 1

算法1：静态分配线性表空间，用指针指向被操作的线性表

Status Insert(Sqlist *L, int i, ElemType e)
{
    if(i<1||i>L.length+1)
        return ERROR;    //i值不合法
    if(L.length>=maxleng)
        return OVERLOW;    //溢出
    for(j=L.length-1;j>=i-1;j--)
        L.elem[j+1]=L.elem[j];    //向后移动元素
    L.elem[i-1]=e;    //插入新元素
    L.length++;    // 长度变量增1
    return OK;
}

　　基本思想：

• 判断插入的位置是否合理；
• 判断表长是否达到分配空间的最大值；
• 从线性表中的最后一个元素到插入位置的所有元素，依次往后移动一个元素的位置，这样给待插入的元素留出了一个空位置；
• 把新增元素插入到这个空位置，表长增加1，返回。

算法2：动态分配线性表空间，用引用参数表示被操作的线性表

int Insert(Sqlist &L, int i, ElemType e)
{
    int j;
    if(i<1||i>L.length+1)
        return ERROR;    //i的合法取值为1至n+1
    if(L.length>=L.listsize)    //溢出时扩充
    {
        ElemType *newbase;
        newbase=(ElemType *)realloc(L.elem, L.listsize+LISTINCREMENT*sizeof(ElemType));
        if(newbase==NULL)
            return OVERFLOW;
        L.elem=newbase;
        L.length+=LISTINCREMENT;
    }
    //向后移动元素，空出第i个元素的分量elem[i-1]
    for(j=L.length-1;j>=i-1;j--)
        L.elem[j+1]=L.elem[j];
    L.elem[i-1]=e;    //新元素插入
    L.length++;    //线性表长度加1
    return OK;
}

插入操作移动元素次数的分析

　　在 (a_1, a₂, ...,a_i-1, a_i ,a_i+1, ..., a_n) 中 a_i 之前插入新元素 e (1<=i<=n)

　　假定 P_i 是在各位置插入元素的概率，且 P₁ = P₂ = ... = P_n = P_n+1 = 1/(n+1)

　　则插入一个元素时移动元素的平均值是：　

 顺序表的删除算法

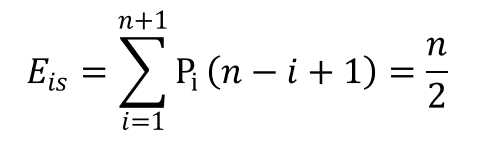
int delete(Sqlist *L, int i)
{
    if(i<1||L->length)
    {
        printf("not exits");
        return ERROR;
    }
    else
        for(j=i;j<=L->length-1;j++)
            L->elem[j-1]=L->elem[j];
    L->length--;
    return OK;
}

　　基本思想：

• 判断删除元素的下标是否存在；
• 用一个for循环来移动元素，移动元素下标范围为 i 到 length-1。
• 修改表长为原表长减1。

删除操作及移动元素次数的分析

　　假定 q_i 是在各位置插入元素的概率，且 q₁ = q₂ = ... = q_n = q_n+1 = 1/n

　　则删除一个元素时移动的平均值是：

顺序结构的优缺点

优点

1. 是一种随机存储结构，存取任何元素的时间是一个常数，速度快；
2. 结构简单，逻辑上相邻元素在物理上也是相邻的；
3. 不需要使用指针，节省存储空间。

缺点

1. 插入和删除元素要移动大量元素，消耗大量时间；
2. 需要一块连续的存储空间；
3. 插入元素可能发生溢出；
4. 自由区中的存储空间不能被其他数据占用（共享），存在浪费空间的问题。

数据结构学习（二）——线性表（一）

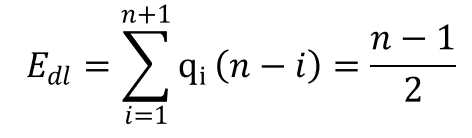
原文：https://www.cnblogs.com/tronysh/p/11694266.html