概率论与数理统计图式（第三章 多维随机变量）

概率论与数理统计图式（第三章 多维随机变量）

1、二位随机变量及其分布

1）二维随机变量定义

设随机试验E 的样本空间为Ω，对于每一样本点ω∈Ω ，有两个实数 X (Ω), Y (Ω) 与之对应，称它们构成的有序数组 ( X , Y ) 为 二维随机变量。

注：对二维随机变量( X, Y )来说， X，Y 都是定义在Ω上的一维随机变量.

2）联合分布函数

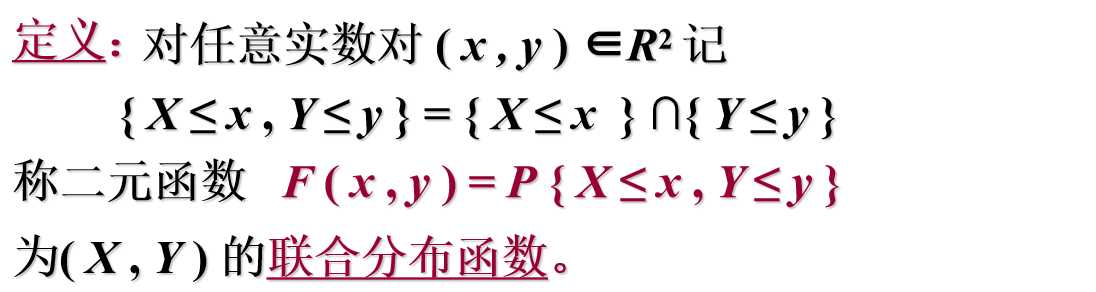
（1）联合分布函数几何意义

平面随机点( X, Y ) 落入以(x, y)为顶点的左下方区域的概率。

（2）联合分布函数的性质

• 单调不减性
• 非负有界性
• 右连续性
• 相容性　　

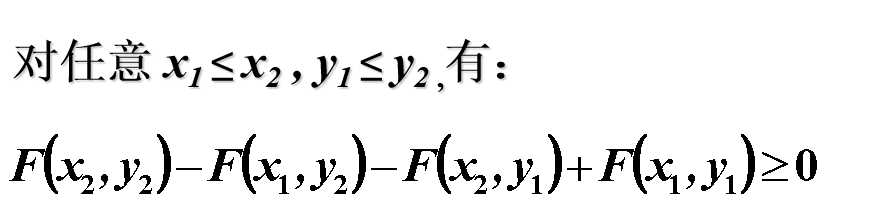
3）边缘分布函数

（1）定义：称X、Y各自 的分布函数 FX(x) 与 FY(y) 为( X, Y ) 的边缘分布函数。

（2）由联合分布函数可确定边缘分布函数：

2、联合分布律

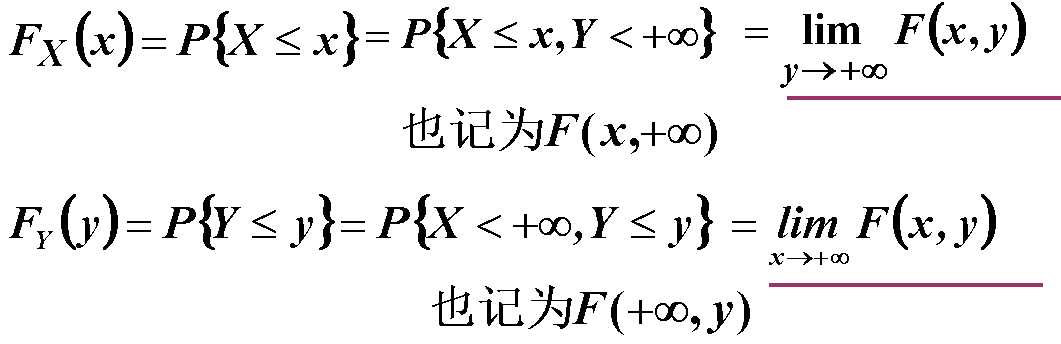
用边缘分布律不一定能确定联合分布律！

原因：多维随机变量的联合分布不仅与每个变量的边缘分布有关，而且还与每个变量之间的联系有关！两个随机变量X,Y不等同于二维随机变量(X,Y)!

3、联合概率密度

（1）联合概率密度的物理解释：概率在(x, y)处的面密度.

（2）联合概率密度曲面

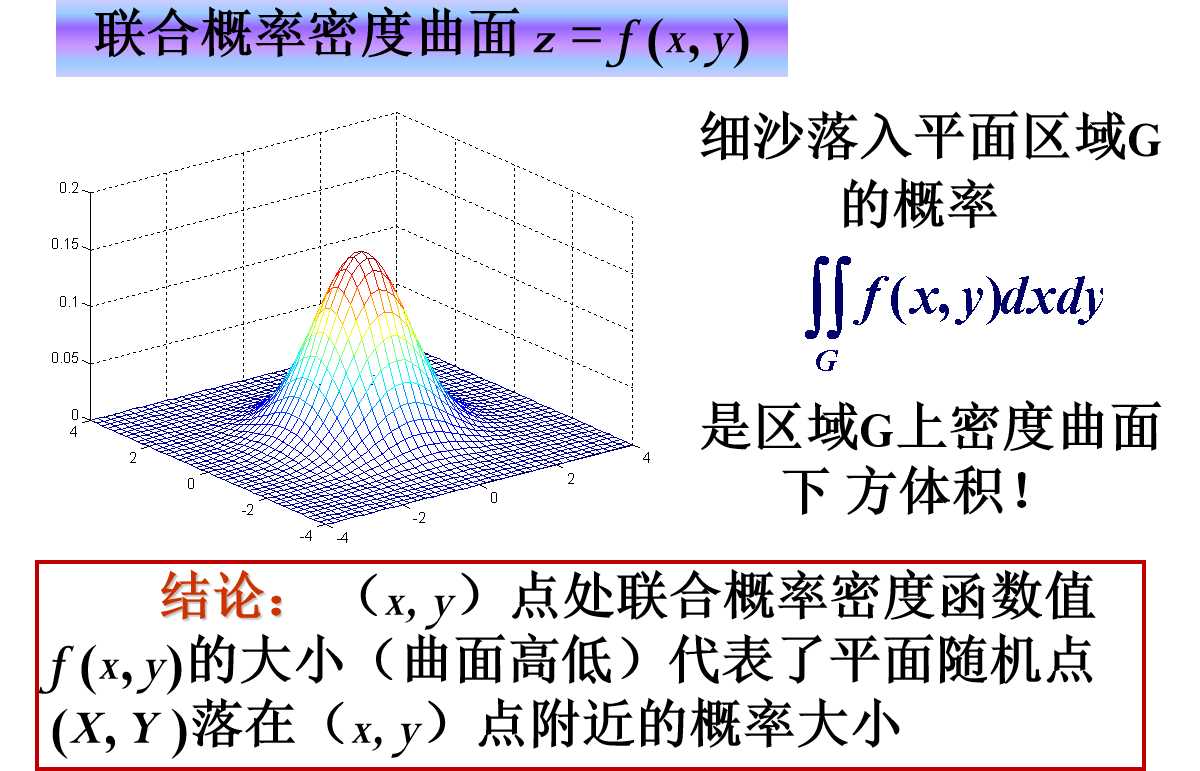
（3）f(x)满足

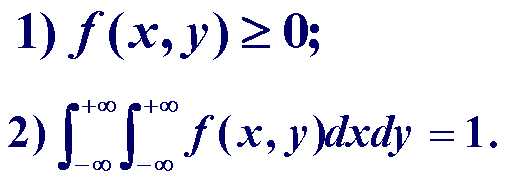
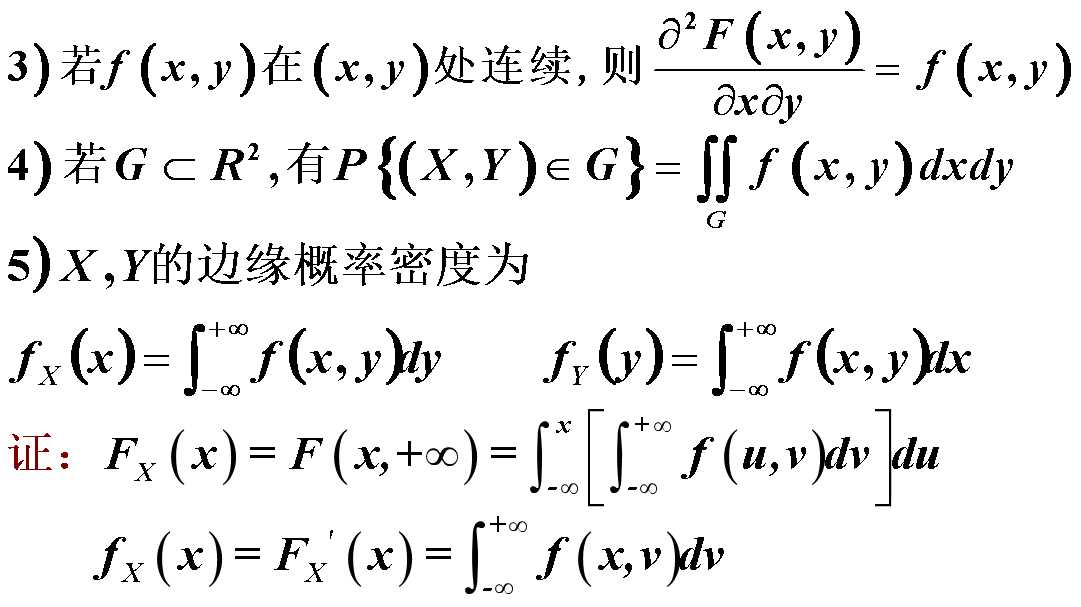
对边缘概率密度的求解,实质上是求带参变量的积分。

难点: 积分上下限的确定!

可通过图形来帮助解决这个问题。

概率论与数理统计图式（第三章 多维随机变量）

原文：https://www.cnblogs.com/ggotransfromation/p/11653744.html