算法的时间、空间复杂度

算法的效率：

　　即算法的运行时间，我们需要一个不依赖于环境的度量指标来描述算法的效率——算法需要执行的步骤数目

大O表示法：

　　描述随着数据量的增加，算法所需时间增加的快慢

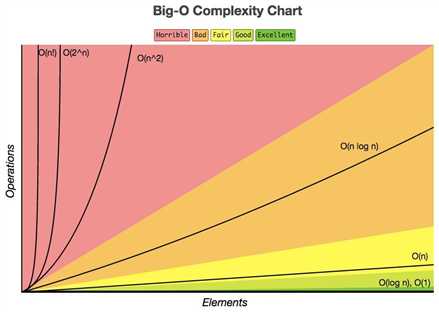
时间复杂度排序：O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)

void eat4(int n){
   for(int i=0; i<n; i++){
       for(int j=0; j<i; j++){
           System.out.println("等待一天");
       }
       System.out.println("吃一寸面包");
   }
}

所需操作次数为：0.5n^2 - 0.5n，我们需要对其进行简化，简化规则如下：

• 如果运行时间是常数量级，用常数1表示
• 去掉运行时间中的所有加法常数
• 只保留最高项
• 如果最高项存在但是系数不是1，去掉系数

最终时间复杂度表示为：O(n^2)

算法的时间、空间复杂度

原文：https://www.cnblogs.com/zsxm/p/11649062.html