先给一道题: [SNOI2017]炸弹
我们发现,一个炸弹可能会影响左右的一些炸弹,然后左右的炸弹又会去影响其他的炸弹。
最暴力的做法当然是向每一个会影响到的炸弹连边。
边会达到n^2,显然无法承受。
然后我们就可以用到一个叫做线段树优化建图的技巧
图片摘自洛谷题解~
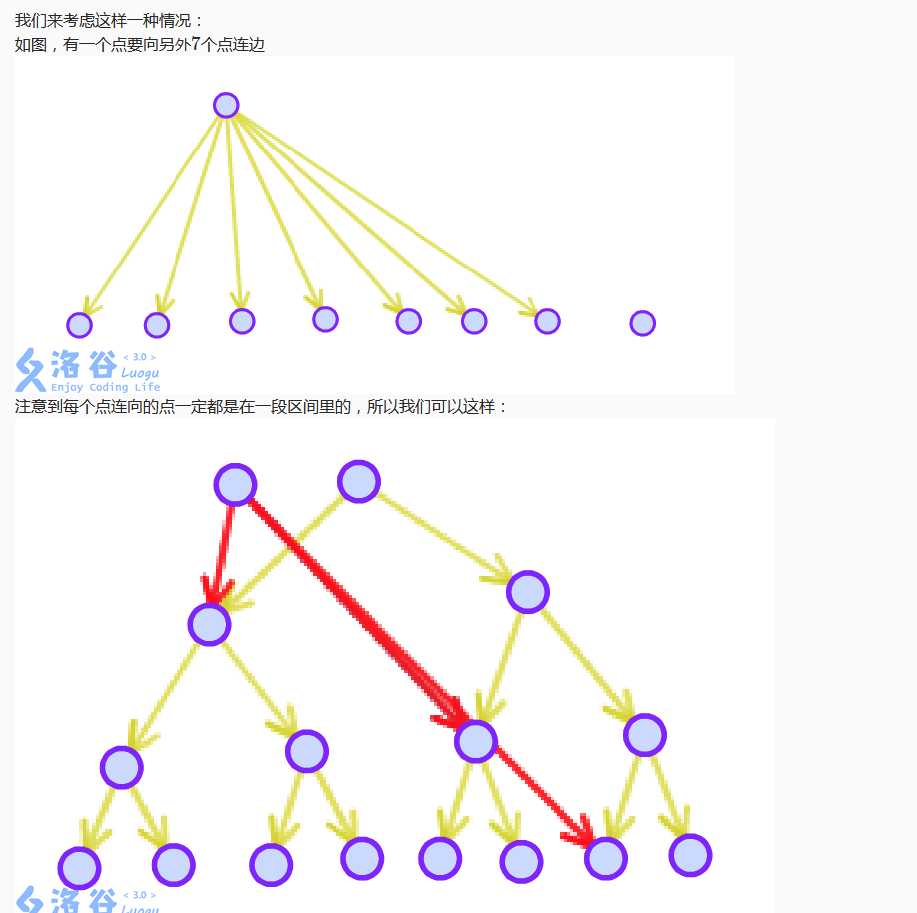
这样边数优化到nlog。
这就是线段树优化建图。
然后对于这道题,需要的还有tarjan缩点,逆向拓扑。
代码算是比较好理解。

#include<bits/stdc++.h> #define mod 1000000007 #define LL long long #define N 500003 using namespace std; LL read() { LL x=0,f=1;char s=getchar(); while(s<‘0‘||s>‘9‘){if(s==‘-‘)f=-1;s=getchar();} while(s>=‘0‘&&s<=‘9‘){x=x*10+s-‘0‘;s=getchar();} return x*f; } void print(LL x) { if(x<0)putchar(‘-‘),x=-x; if(x>9)print(x/10); putchar(x%10+‘0‘); } struct EDGE{ int nextt,to,me; }w1[20*N],w2[20*N]; LL b[N],a[N],r[N],minn[N*4],maxx[N*4]; int lc[N*4],rc[N*4],stackk[N*4],vis[N*4],id[N*4],di[N*4],low[N*4],dfn[N*4],belong[N*4],in[N*4]; int head1[N*4],head2[N*4]; int ndnum=1; int pp; int cur,cnt,top; int tot1=0,tot2=0; void add1(int a,int b) { tot1++; w1[tot1].nextt=head1[a]; w1[tot1].me=a; w1[tot1].to=b; head1[a]=tot1; } void add2(int a,int b) { tot2++; w2[tot2].nextt=head2[a]; w2[tot2].me=a; w2[tot2].to=b; head2[a]=tot2; } void build(int k,int l,int r) { pp=max(pp,k); if(l==r){id[l]=k;di[k]=l;return;} int mid=(l+r)>>1; build(lc[k]=++ndnum,l,mid); build(rc[k]=++ndnum,mid+1,r); add1(k,lc[k]);add1(k,rc[k]); } void update(int k,int L,int R,int l,int r,int x) { if(L==l&&R==r){add1(x,k);return;} int mid=(L+R)>>1; if(l>mid)update(rc[k],mid+1,R,l,r,x); else if(r<=mid)update(lc[k],L,mid,l,r,x); else { update(lc[k],L,mid,l,mid,x); update(rc[k],mid+1,R,mid+1,r,x); } } void tarjan(int x) { low[x]=dfn[x]=++cur; stackk[++top]=x; vis[x]=1; for(int i=head1[x];i;i=w1[i].nextt) { int id=w1[i].to; if(!dfn[id])tarjan(id),low[x]=min(low[x],low[id]); else if(vis[id])low[x]=min(low[x],dfn[id]); } if(low[x]==dfn[x]) { cnt++; int t; minn[cnt]=4e18; maxx[cnt]=-4e18; do{ t=stackk[top--]; vis[t]=0; belong[t]=cnt; if(di[t]) { minn[cnt]=min(minn[cnt],a[di[t]]-r[di[t]]); maxx[cnt]=max(maxx[cnt],a[di[t]]+r[di[t]]); } }while(t!=x); } } queue<int>q; int main() { int n=read(); for(int i=1;i<=n;++i) b[i]=a[i]=read(),r[i]=read(); build(1,1,n); sort(b+1,b+1+n); int num=unique(b+1,b+1+n)-(b+1); for(int i=1;i<=n;++i) { int x=lower_bound(b+1,b+1+num,a[i]-r[i])-b; int y=upper_bound(b+1,b+1+num,a[i]+r[i])-b-1; update(1,1,n,x,y,id[i]); } for(int i=1;i<=pp;++i) if(!dfn[i])tarjan(i); for(int i=1;i<=tot1;++i) { if(belong[w1[i].me]==belong[w1[i].to])continue; add2(belong[w1[i].to],belong[w1[i].me]);//逆向拓扑 in[belong[w1[i].me]]++; } while(!q.empty())q.pop(); for(int i=1;i<=cnt;++i) if(!in[i])q.push(i); while(!q.empty()) { int x=q.front();q.pop(); for(int i=head2[x];i;i=w2[i].nextt) { int v=w2[i].to; in[v]--; if(!in[v])q.push(v); minn[v]=min(minn[v],minn[x]); maxx[v]=max(maxx[v],maxx[x]); } } LL ans=0; for(int i=1;i<=n;++i) { int l=lower_bound(b+1,b+1+num,minn[belong[id[i]]])-b; int r=upper_bound(b+1,b+1+num,maxx[belong[id[i]]])-b-1;//注意是id[i],minn/maxx是存在对应标号里的 LL res=(LL)(r-l+1)*i%mod; ans=(LL)(ans+res)%mod; } printf("%lld\n",ans); } /* */
原文:https://www.cnblogs.com/yyys-/p/11628690.html