向量叉积

定义

\[\vec a\times\vec b=|\vec a||\vec b|sin\theta\]

证明

• 证明：在如图所示的平行四边形0ACB中 \[S_{\Delta AOC}=\frac{1}{2}|\vec {a}||\vec b|sin \theta\]
• 则平行四边形的面积是 \[S=|\vec{a}| |\vec b|sin\theta\]
  \[\vec a \cdot \vec b=|\vec a| |\vec b| cos \theta\]
  \[cos\theta=\frac{\vec a \cdot \vec b}{|\vec a| |\vec b|}\]

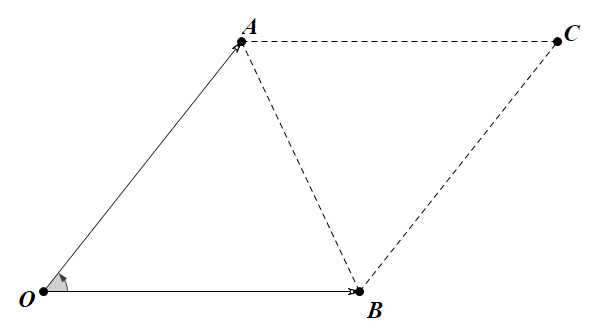
\[ \begin{eqnarray} sin\theta &= & \sqrt{1-cos^2\theta} \&=&\frac{\sqrt{(|\vec a|^2\cdot|\vec b|)^2-(\vec{a}\cdot{\vec{b})^2}}}{|\vec a||\vec b|} \\end{eqnarray} \]

\begin{eqnarray}
S &=& \sqrt{(|\vec a|^2\cdot|\vec b|)^2-(\vec{a}\cdot{\vec{b})^2}} \
&=& \sqrt{(x_1^2+y_1^2)(x_2^2+y_2^2)-(x_1x_2+y_1y_2)^2} \
&=& \sqrt{(x_1y_2)^2+(x_2y_1)^2-2x_1x_2y_1y_2} \
&=& \sqrt{(x_1y_2-x_2y_1)^2} \
&=& |x_1y_2-x_2y_1| \
\end{eqnarray}

向量叉积

原文：https://www.cnblogs.com/Vimin/p/11627515.html