Josephus

第二次坑在了约瑟夫问题上，话说模拟的约瑟夫我还没过掉，emmm

 题目：一开始有 n 个人围成一个圈, 从 1 开始顺时针报数, 报出 m 的人被机关处决. 然后下一个人再从 1 开始报数, 直到只剩下一个人. 

只讲公式递推法喽

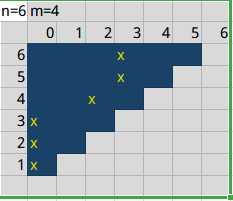
 首先，钦定序列的下标全部减一，为了取模运算不需特判0的情况

把每次操作的序列按时间放在一起是一个倒三角形状，考虑倒推，那么最后一次也就是长度为1时，x在最后一次的那个序列里为0。考虑把它转移到长度为2，即求出在长度为2时，x在这个序列里的位置。长度为1的序列的第一个点，相当于这个点在len=2的序列中，它的前面的点，要么被删出去了，要么挪到了这个点的后面，然后只要找到在len=2时，len=1的1点的位置，那么，就有了x在len=2时的位置

转移len=i式子为$pos=(m+pos)\ mod\ i$

简单口胡：

先找到len=i-1序列中1在len=i序列中位置，为$(m-1)\ mod\ i$

然后在这个位置数pos-1个，$pos=((m-1)\ mod\ i+pos-1)\ mod\ i$

递退到最后，答案为pos+1

至于模拟题

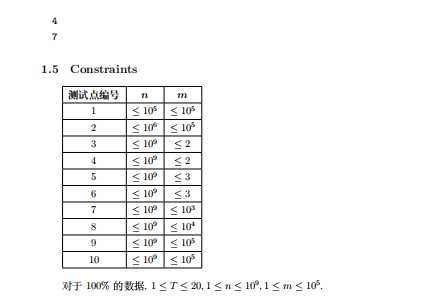
n<=1e9，需要一个有效的优化，考虑柿子$pos=(pos+m)\ mod\ i$中取模在大部分时间可能没用

结合图可以发现，随着i在变大，+m越来越不能使pos跳到前面，那么可以算一个k使得pos可以直接跳一大段

则有不等式$k*m+pos<k+i-1$，每次算出即可

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std;
 5 inline int minn(int a,int b){return a<b?a:b; }
 6 int T,n,m;
 7 int main(){
 8     //freopen("da.in","r",stdin);
 9     scanf("%d",&T);
10     while(T--){
11         scanf("%d%d",&n,&m);
12         int pos=0;
13         for(int i=2,k;i<=n;){
14             //k*m+pos<k+i
15             //pos=(m+pos)%i;
16             //cout<<(i-pos-1)/(m-1)-1<<endl;
17             k=0;
18             if(((i-pos-1)/(m-1)-1)>=0)k=minn(n-i+1,(i-pos-1)/(m-1)-1);
19             i+=k;pos+=k*m;
20             //cout<<i<<" "<<pos<<endl;
21             if(i<=n){
22                 pos=(pos+m)%i;
23                 ++i;
24             }
25         }
26         printf("%d\n",pos+1);
27     }
28     return 0;
29 }

View Code

 来自迪神

至于时间复杂度，肯定O(能过)，简单研究一下发现，在len<=m，那么每次只能减1，当len>m时，几乎都是每次$*(\frac{m-1}{m})$，即为$n*(\frac{m-1}{m})^k=m$

为$O(m+log_{\frac{m}{m-1}}\frac{n}{m})$

Josephus

原文：https://www.cnblogs.com/2018hzoicyf/p/11624950.html