特征方程求线性递推方程的通项公式

问题引入

设有递推方程 f(n)=k₁*f(n-1)+k₂*f(n-2)，已知k₁,k₂及f(0),f(1)，给定n求f(n)

解法

1.O(n)直接递推

2.O(m³ * log₂n)矩阵快速幂（m为矩阵大小）

3.求f(n)通项公式,O(log₂n)快速幂（或光速幂）

求通项公式

前提：已知线性递推方程；已知f中某两项

步骤：

1.上述递推式的特征方程为x²=k₁*x+k₂（用x²替换f(n)，x替换f(n-1)，1替换f(n-2)），解此一元二次方程的两解x₁,x₂；

2.f(n)的通项公式为f(n)=α*x₁ⁿ+β*x₂ⁿ，只需解出α,β；

3.带入已知得两项比如f(0),f(1)得关于α,β得二元一次方程组，即可解出α,β。

举例：

1.f(n)=f(n-1)+f(n-2),f(0)=0,f(1)=1,求f(n)通项公式（斐波那契数列）

特征方程为x²=x+1，解得x=(1±√5)/2；

f(n)=α*[(1+√5)/2]ⁿ+β*[(1-√5)/2]ⁿ；

带入 f(0)=1,f(1)=1,得α=√5/5，β=-√5/5；

所以f(n)=√5/5*[(1+√5)/2]ⁿ-√5/5*[(1-√5)/2]ⁿ;

2.f(n)=233*f(n-1)+666*f(n-2),f(0)=0,f(1)=1,求f(n)通项公式

特征方程为x²=233*x+666，解得；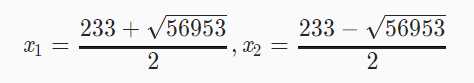

则f(n)=α*x₁ⁿ+β*x₂ⁿ

带入f(0)=0,f(1)=1,得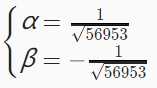

 所以f(n)=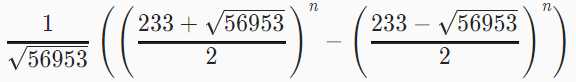

关于光速幂 

例题：洛谷P5510

参考文章：

1.https://blog.csdn.net/qq_20340417/article/details/78433961

2.https://www.luogu.org/blog/xgzc/solution-p5110

3.https://blog.csdn.net/qq_35950004/article/details/85378226

特征方程求线性递推方程的通项公式

原文：https://www.cnblogs.com/lllxq/p/11614477.html