二叉树、满二叉树、完全二叉树

定义

树的结点（node）：包含一个数据元素及若干指向子树的分支；

孩子结点（child node）：结点的子树的根称为该结点的孩子；

双亲结点：B 结点是A 结点的孩子，则A结点是B 结点的双亲；

兄弟结点：同一双亲的孩子结点； 堂兄结点：同一层上结点；

祖先结点: 从根到该结点的所经分支上的所有结点

子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙

树的深度：树中最大的结点层

结点的度：结点子树的个数

树的度： 树中最大的结点度。

叶子结点：也叫终端结点，是度为 0 的结点；

分枝结点：度不为0的结点；

二叉树

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

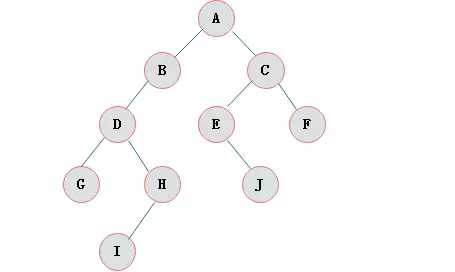
 特点：

1.每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。

2.左子树和右子树是有顺序的，次序不能任意颠倒。

性值：

1.在二叉树的第i层上最多有2^i-1 个节点 。（i>=1）

2.二叉树中如果深度为k,那么最多有2^k-1个节点。(k>=1）

3.n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。 即叶子节点 = 双分支节点数+1

满二叉树

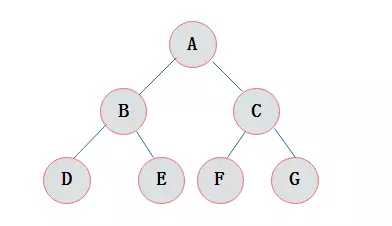
在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

特点：

1.叶子只能出现在最下一层。出现在其它层就不可能达成平衡。

2.非叶子结点的度一定是2。

3.满二叉树的叶子节点 = 2^k-1

完全二叉树

对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

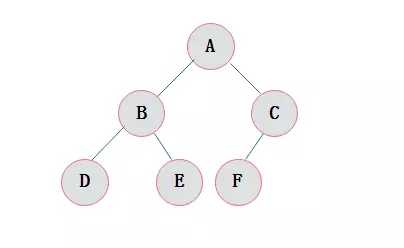
特点：

1.叶子结点只能出现在最下层和次下层。

2.最下层的叶子结点集中在树的左部。

3.倒数第二层若存在叶子结点，一定在右部连续位置。

4.如果结点度为1，则该结点只有左孩子，即没有右子树。

5.同样结点数目的二叉树，完全二叉树深度最小。

 需求：创建以可完全二叉树，并实现 前、中、后、层 四种遍历输出（C语言实现）

二叉树、满二叉树、完全二叉树

原文：https://www.cnblogs.com/baizhuang/p/11612935.html