贝叶斯网络之----（d-分离步骤）

贝叶斯网络假设是指给定一个变量的父母节点，这个变量条件独立于他的非后代。

d-separation步骤用途

回答两类问题，

1. 给定变量下条件独立性问题。例如，在给定D和F的情况下，A和B是否独立，$ P(A|BDF) = P(A|DF)$ 。
2. 边际独立性问题。例如，A和B是否独立，$ P(A|B) = P(A)$ 。

d-separation步骤流程

1. 概率表达式中所提到节点及其祖先（不带子女，除非提到）组成的图。
2. 父母配用无线边配对。
3. 将所有边变成无向边。
4. 删除所有给定变量的节点，以及他们的边。例如，在给定D和F的情况下，A和B是否独立，$ P(A|BDF) = P(A|DF)$ 。那么要删去的节点就是D和F。
5. 解释得到的图。经过前面4步得到一个图，如果a）变量是不连接的，则独立或条件独立性满足，如果b）变量在图中是连接的。则不能保证独立或条件独立性。这里连接指的是节点之间存在一条路径。c）如果一个或多个变量在图中不存在，则独立或条件独立性满足。

熟练之后，可知两个没有公共祖先的节点是边际独立的，但给定他们的子节点，他们就变成相关的（common effect）例如下图情形，

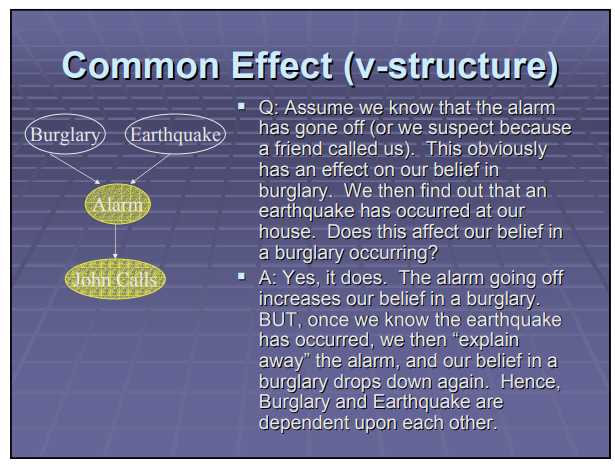
下两个图是相关路径（active trails）几种情形，以及基于相关路径的两节点d-separation定义（应该和我们用上述流程得到的连接或不连接是一致的，这个是在另一个文献里找的），

d-separation步骤例子

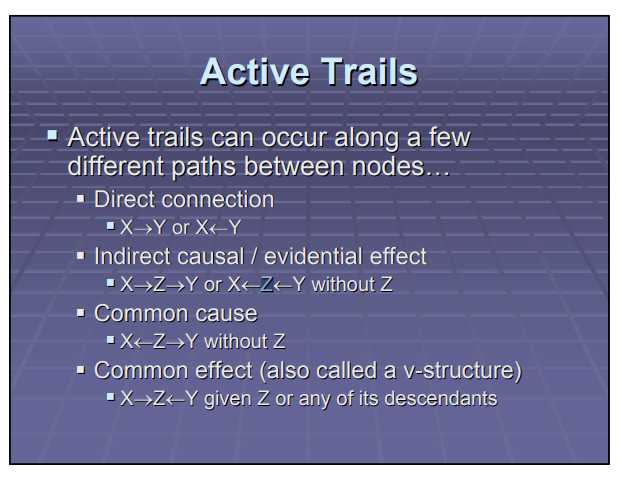
给一个概率图，如下

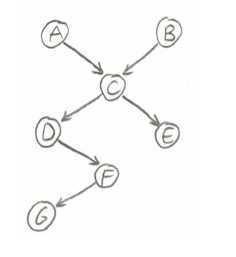
则，

1. 在给定D和F的情况下，A和B是否独立，即是否有 $ P(A|BDF) = P(A|DF)$ ？

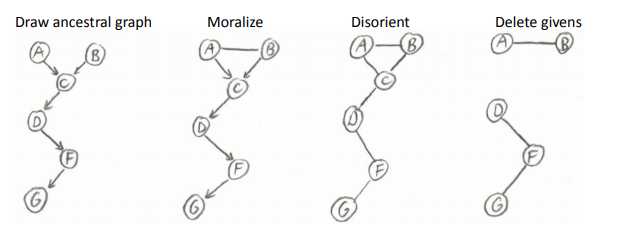
   否。四步走，如图，

   

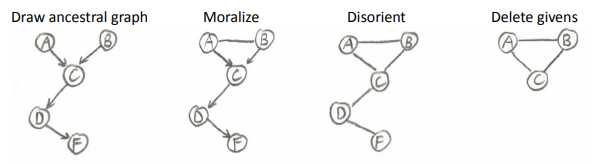
2. A和B是否（边际）独立，即 $ P(A|B) = P(A)$ ？

   是。看图，

   

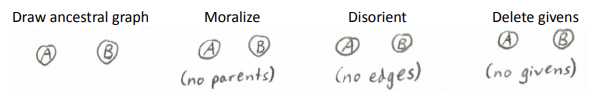
3. 给定C的情况下，A，B独立吗？

   否，上面提到的有名的V-结构（common effect），看图，应用步骤时注意与问题2区别，

   

4. 给定C的情况下，D,E独立吗？

   是，朴素贝叶斯条件独立性假设就是这种共同祖先结构！注意，画一个点必须画他的祖先，但没有提到他的子女，就不画她的子女。看分析，

   

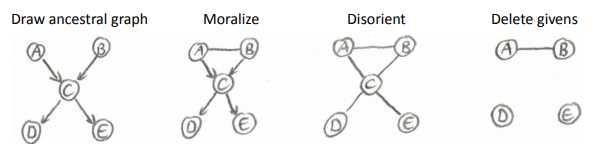
5. D,E独立吗？

   否，

   

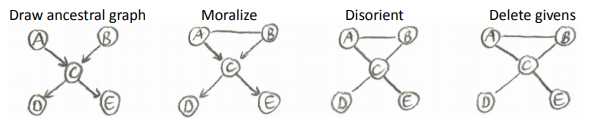
6. 给定A，B的情况下，D,E独立吗？

   否，不同于给定C的情形，

   

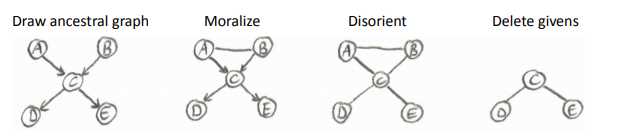
7. $ P(D|CEG) = P(D|C)$ ？

   转换成两个问题，a给定C时，D,E独立吗？且b给定C时，D,G独立吗？

   a是b否总体否

   

参考链接：

d-separation procedure

no active trial

今天很郁闷，我觉得自己很失败。但我还是要不停的做事情。

越是绝望，越是不能停止做事情。

好熟悉面孔,是哪部剧来着...

贝叶斯网络之----（d-分离步骤）

原文：https://www.cnblogs.com/qizhien/p/11604594.html