1.实践题目:输入n值(1<=n<=1000)、n个非降序排列的整数以及要查找的数x,使用二分查找算法查找x,输出x所在的下标(0~n-1)及比较次数。若x不存在,输出-1和比较次数。
提交的代码:
#include<iostream>
using namespace std;
int Search (int a[],int n, int x,int &t)
{
int l = 0;
int r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (x == a[mid]) {
t++;
return mid;
}
if (x > a[mid]) {
t++;
l = mid + 1;
} else {
t++;
r = mid - 1;}
}
return -1;
}
int main()
{
int n;
int a[1000];
int x,t = 0;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
cin >> x;
cout << Search (a, n, x, t)<<endl;
cout << t;
return 0;
}
第一道题思路其实很简单,就是二分法找目标数字,不过不知道是什么原因,在给调用函数传参的时候总是编译器报错,最后又打了几次又莫名其妙可以了,应该是基本代码能力还缺了点吧。
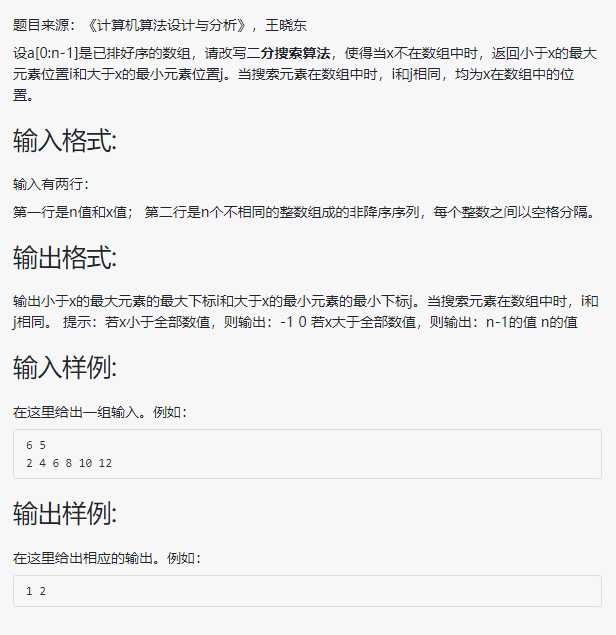
然后第二题,
首先,读题:就是不存在指定数value时,就输出小于x的最大元素位置i和大于x的最小元素位置j,其实在这里可以发现,当二分递归出来的结果l,即使找不到,也是小于x的最大元素位置i,那么求大于x的最小元素位置j只需要加1即可,对于特别的点,只需要进行一些简单的特判,就可以过了。
#include<iostream>
using namespace std;
int BIN(int a[], int key, int n) {
int left = 0;
int right = n - 1;
int i = 0;
int j = 0;
while (left <= right) {
int middle = (left + right) / 2;
if (key == a[middle])
{
i = j = middle;
cout << i <<" "<<j<<endl;
//cout << t;
return middle;
}
if (key > a[middle])left = middle + 1;
else { right = middle - 1; }
}
i = right;
j = left;
cout << i<<" "<< j<<endl;
return -1;
}
int main() {
int n;
int x;
cin >> n>> x;
int *a = new int [n];
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
BIN(a, x, n);
system("pause");
}
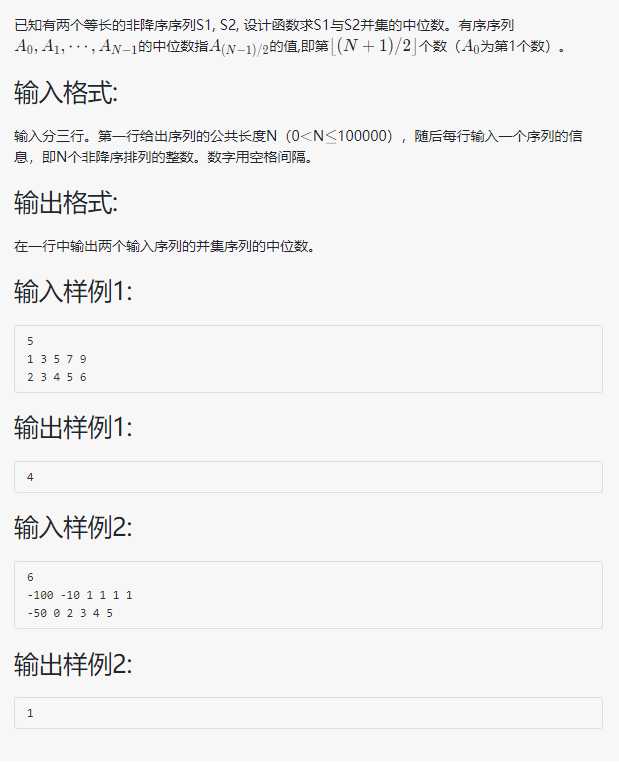
第三题课上并没有来得及看,课后和partner一起打的时候大概理清了思路
如果两段序列的中位数,都是相等的话,那么中位数即为该数。
如果当第一段的中位数大于第二段的时候,那么两端合中位数一定在第一段中位数前或第二段中位数后,这时只取这两部分,再继续进行二分比较
如果当第一段的中位数小于第二段的时候,那么两端合中位数一定在第一段中位数后面或第二段中位数前面,这时只取这两部分,再继续进行二分比较

最后总结一下对二分法的看法
二分搜索看起来思路挺简单的,但是在执行过程中,总会有一些细节上的小错误,在这次的实验过程种也感受到了:
1 边界点的等号是否取到,中间点的位置是否可取
2 二分的对象该如何妥当处理
原文:https://www.cnblogs.com/strelitzia/p/11575725.html