朴素贝叶斯(分类)

\begin{aligned}
P(C|F)=\frac{P(F|C)P(C)}{\sum_iF_i}=\frac{\prod_iP(F_i|C)P(C)}{\sum_iF_i}
\end{aligned}

• \(C\): Class, 类别
• \(F\): Feature，特征
• \(P(C)\): 先验概率
• \(P(F|C)\)：似然值
• \(\sum_iF_i\)：归一化用的，对所有类别都相同，可忽略
• 假设“所有特征彼此独立”，问题转化为：
  \begin{aligned}
  P(C|F)\propto\prod_iP(F_i|C)P(C)
  \end{aligned}
  其中\(P(F_i|C)\)和\(P(C)\)可从统计资料中得到，由此可计算出每个类别对应的概率，从而找出最大概率的类。
• “所有特征彼此独立”是很强的假设，现实中不太可能成立，但是可以大大简化计算，且有研究表明对分类结果准确性影响不大。

参考：阮一峰的网络日志

决策树(分类)

算法核心

选择最优的划分特征。每次划分后的分支节点所包含的样本尽可能的属于同一类别，也就是节点中所包含的样本纯度越来越高。

如何评判纯度？

信息熵

信息量化

如何衡量\(H(x)\)的大小

1. 事件的信息量和事件发生的概率有关。\(H(x)\Leftrightarrow \frac{1}{P(x)}\)
2. 多个事件的信息总量是信息量的加和。\(H(x_1,x_2)\Leftrightarrow H(x_1)+H(x_2)\)
3. \(H(x)\ge0\)

需要构造一个关于\(H(x)\)的函数满足上述关系：\(H(x)=log \frac{1}{P(x)}=-logP(x)\)

熵

熵求的是\(H(x)\)在\(P(x)\)分布下的数学期望，代表一个系统的不确定性，信息熵越大，不确定性越大。
\begin{aligned}
Entropy(x) = E_x[H(x)]=-\sum_xP(x)logP(x)
\end{aligned}

• 全为一种元素，熵最小，\(Entropy(x)=0\)
• 系统内元素均匀分布，熵最大，\(Entropy(x)=1\)
• 想在系统内对元素划分，使得同一类元素在一起，每次划分就希望 minimize 系统的信息熵

信息增益

Information Gain(IG)

\begin{aligned}
IG=OriginalEntropy - \sum_i \frac{A_i}{|A|}Entropy(A_i)
\end{aligned}
信息熵是系统的不确定度，信息增益代表划分后系统的不确定度减少的程度。

每次划分希望信息增益越大越好。

ID3算法

采用 Information Gain 作为纯度的度量，算每一个特征的信息增益，选择使得信息增益最大的特征进行划分。

决策树划分

特征类型：

1. ordinal 离散而有序
2. numerical (discrete nominal) 离散而无序
3. continuous 连续

贝叶斯分类模型适用离散无序类型(discrete)的特征

划分方法：

1. 多路划分
   • 独立值
2. 二分法
   • 组合

Discretization 连续数据离散化：

1. 有序离散化
   • 静态划分 一开始就离散化
   • 动态划分 均匀间隔、均匀频次、聚类
2. 二分法
   • 类似IG3算法划分，找IG最大的划分
   • 计算更密集

Gini Index

除了熵，还有其他方式来指导决策树划分。
\begin{aligned}
GINI(t)=1-\sum_jP(j|t)^2
\end{aligned}
\(P(j|t)\)：每个状态\(t\)里每个class\(j\)的频率

• 若均匀分布(对应熵 = 1的情况)，GINI Index = 0.5 最大
• 若某一类元素占比为1 (对应熵 = 0的情况)，GINI Index = 0 最小

比较容易算，不用计算log。

Gini Split

划分\(k\)个分区，计算各个分区的加权 GINI 指数

对应信息增益

\begin{aligned}
GINI_{split}=\sum_{i=1}^k\frac{n_i}{n}GINI(i)
\end{aligned}

• \(n_i\)：当前分区内元素个数
• \(n\): 系统内总的元素个数

GINI划分越小越好

Misclassification Error

错分率

\begin{aligned}
Error(t)=1-max_iP(i|t)
\end{aligned}

• \(P(i|t)\)：每个状态\(t\)里每个class\(i\)的频率
• 若某一类元素占比为1 (对应熵 = 0，GINI Index = 0的情况)，Error = 0 最小
• 若均匀分布(对应熵 = 1，GINI Index = 0.5的情况)，Error = 0.5 最大

Traning and Test Errors

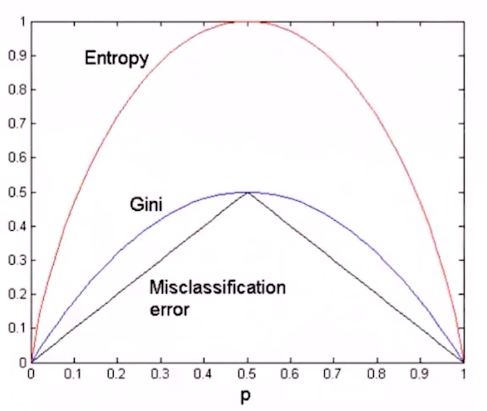
训练决策树时什么时候该停止，停止过早，没有很好学习数据性能，停止过晚，过拟合现象。

Tree Ensemble 集成学习

numbers of nodes： complexity of model

CART回归树(预测)

预测回归连续型数据。

给定训练数据 \(D={(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})}\)，希望学习一个CART树来最小化损失函数

\begin{aligned}
Loss = min_{j,s}[min_{C_1}L(y^i,C_1)+min_{C_2}L(y^i,C_2)] \newline
where \quad C_m=ave(y_i|x_i \in R_m)
\end{aligned}

• \(R_m\)：被划分的输入区间
• \(C_m\)：区间\(R_m\)对应的输出值
• \(L\): \(y\)和\(C\)之间的距离
• \(y\)：第几个特征变量
• \(s\): 分割点
• 遍历特征变量\(j\)，在每一个特征变量上选择合适分割点，使得距离相加和最小，最后选择最好的结果对应的\(j\)和\(s\)
• cost functin : 每一个区间的均值和\(y\)之间的距离
• 计算距离一般常用\(L_2\)欧式距离
• CART树一般就分2块区域，\(R_1\)和\(R_2\)，因为是递归分割的

集成学习

Bagging (Bootstrap Aggregating，引导聚集算法，装袋算法)

• 给定大小为\(n\)的训练集\(D\)，从中均匀、有放回地选出\(m\)个大小为\(n'\)的子集\(D_i\)作为新的训练集。在这\(m\)个训练集上使用分类、回归等算法，则得到\(m\)个模型，再通过取平均值、取多数票等方法，即可得到 Bagging 结果。
• 采好后每一个定形处理

• 很好做并行

• Bagging 算法可与其他分类、回归算法结合，提高准确率、稳定性的同时，通过降低结果的方差，避免过拟合的发生。

• Bootstrap 是统计学里一种采样方法。自身有放回式采样。

Random Forest

对CART树使用 Bagging 算法，生成的许多树组成随机森林。

Boosting(增强算法)

AdaBoost

给出训练数据\(D={(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})}\)，\(x^{(i)}\in R^n\)，\(y \in \left\{ +1,-1 \right\}\)。对每一个\(x^{(i)}\)，有一个相应的权重\(w^{(i)} \in R\)(标量)

1. 初始化

\begin{aligned}
w=(w^{(1)},w^{(2)},...,w^{(N)})\newline w^{(i)}=\frac{1}{N},\quad i=1,2,...,N
\end{aligned}

1. for \(k=1,2,...,K\)迭代

\(G_k(x)\)是一个弱分类器(朴素贝叶斯、决策树)

1. 计算每个弱分类器的错分率

\begin{aligned}
e_k=P(G_k(x^{(i)})不等于 y^{(i)})\newline =\sum_iw^{(i)}I (G_k(x^{(i)}不等于 y^{(i)} )
\end{aligned}

• \(I(condition)\)：Indicator 指示函数，逻辑变量，括号内等式成立等于1，不成立等于0。这里表示被分类错误的样本数量。
• \(w^{(i)}\)：初始化状态是\(\frac{1}{N}\)

1. 计算每个弱分类器的权重
   \begin{aligned}
   \alpha_k = \frac{1}{2}ln(\frac{1-e_k}{e_k})
   \end{aligned}

• 如果一个分类器的误差比较大，不希望该分类器的权重较大

1. 更新训练数据权重\(w^{(k)}\)
   \begin{aligned}
   w_{k+1}^{(i)}=\frac{w_k^{(i)}}{z_k}exp(-\alpha_ky^{(i)}G_k(x^{(i)})
   \end{aligned}

• \({z_k}\)：归一化处理，使得\(w_k^{(i)}\)加和为1。
  \begin{aligned}
  {z_k}=\sum_{i=1}^N w_k^{(i)}exp(-\alpha_kG_k(x^{(i)})
  \end{aligned}

1. 得到结果
   \begin{aligned}
   f(x)^{(i)}=\sum_{k=1}^k\alpha_kG_k(x^{(i)})
   \newline
   F(x^{(i)})=sign(f(x)^{(i)}) \quad最终分类结果
   \end{aligned}

• sign()函数，大于0输出1，小于0输出-1

Boosting需要逐个训练弱分类器，1）数据权重初始化 。2）根据每一个弱分类器的误差来算数据的新权重，分错了权重增加，分对了权重减少。3）将要分类的数据输入到每一个弱分类器，由每一个若分类器的加权结果得出最终结果。

Gradient Boosting(梯度提升)

boosting的思想：分类器对分对了的保留，分错了的在下一个分类器加强学习。每次都在调整残差。

Gradient Boosting： 每一次建立模型是在之前建立模型损失函数的梯度下降方向.

有损失函数就会有梯度

在函数空间求梯度

1. 给定训练数据 \(D={(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})}\)，我们要让残差适应之前的弱分类器

\begin{aligned}
F_{m+1}(x) = F_{m}(x)+h(x)
\end{aligned}
我们的目标是学习一个\(h(x^{(i)})\)：

\begin{aligned}
F_{m+1}(x^{(i)})=F_{m}(x^{(i)})+h(x^{(i)})=y^{(i)}
\end{aligned}

1. 监督学习，目的是找到一个对于$ F(x)\(的逼近函数\)\widehat F(x)$, 通过最小化损失函数的数学期望

\begin{aligned}
\widehat F(x)=argminE_{x,y}[L(y,F(x))]
\newline
F(x)=\sum_{i=1}^M \alpha_ih_i(x)
\newline
F_0(x)=argmin_C\sum_{i=1}^NL(y^{(i)},C)
\newline
F_m(x)=F_{m-1}(x)+argmin\sum_{i=1}^N[L(y^{(i)},F_{m-1}(x^{(i)})+h_m(x^{(i)}))
\end{aligned}

• \(argmin\): 使后面的式子达到最小值时的变量的取值
• \(F_0(x)\)：对于CART树来说就是初始情况，学习一个常数C即可
• 有了\(F_0(x)\)，下一部分就是加上误差函数和残差

1. 学习残差

\begin{aligned}
r_m^{(i)}=-[\frac{\partial L(y^{(i)},F(x^{(i)}))}{\partial F(x^{(i)})}]
\end{aligned}

• 负导数就是改进梯度方向

1. 学习决策树拟合残差
   学习一个CART树来拟合残差
   \begin{aligned}
   C_{mj}=argmin_C \sum_{x \in k(m,j)} L(y^{(i)}, F_{m-1}(x^{(i)})+C)
   \end{aligned}

机器学习经典模型

原文：https://www.cnblogs.com/ColleenHe/p/11564768.html