先吐槽一下我的民科老师吧,要不是你,我tm也不用自学一遍离散.脏话。
要想学好算法,先学离散,我的学校课程安排也不合理,一般都是先ds再离散的,我学校偏偏反着来,呵呵
————————————————————————————————————————————————————————————
二元关系顾名思义就是两个元素之间的关系,(关系就是集合)
像这样的<x,y>的有序的二元组(向量)叫有序对,
设A,B为集合,A中的元素为第一个元素,B中的元素为第二个元素,的集合叫笛卡尔(就是那个说我思故我在的家伙)集,。记作A*B。
如果一个集合为空或为笛卡尔集则称这个集合为二元关系,简称为关系,
设A,B为集合,A*B的任意子集所定义的关系称为从A到B的二元关系,当A=B时称为A上的二元关系,
对于任意集合A,空集是A*A的子集,称作A上的空关系,
对于任意集合A,有:
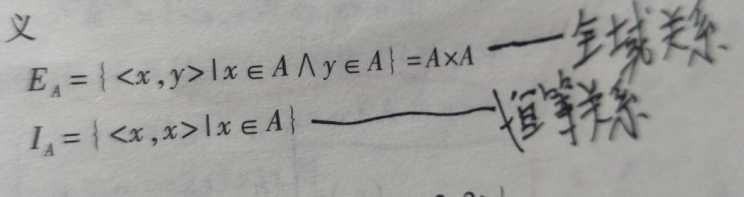
偷一下懒
对于x,y我们还可以定义其他关系比如x>y,则称小于关系等等
————————————————————————————————————————————————
关系的表述方法————集合表达式,关系矩阵和关系图。
————————————————————————————————————————————————
关系的运算


——————————————————————————————————————————————————————
关系的性质
自反,反自反,对称,反对称,传递。
这个课本上说的太抽象了,我用通俗的描述一下
假设集合A,以及基于A上的关系R
自反: 如果a是A的元素,那么<a,a>是R的元素
反自反:如果a是A的元素,那么<a,a>不是R的元素
对称: 如果<a,b>是R的元素,那么<b,a>是R的元素
反对称:如果<a,b>,<b,a>是R的元素,那么a,b相等
传递: 如果<a,b>,<b,c>是R的元素,那么<a,c>是R的元素
———————————————————————————————————————————————————————
关系的闭包
设R是A上的关系,我们希望R具有某些有用的性质,比如自反性,如果不具有则我们可以往R中添加一些有序对来改造R成为R1,
是R具有自反性,但有要求添加的有序对尽量少,满足自反性的R1就称为R的自反闭包,
或者还可以求对称闭包,传递闭包等。
算法 下次
————————————————————————————————————————————————————————
等价关系与划分
设R为非空集合A上的关系,如果R是自反,对称,传递的则称R为A上的等价关系,设R是一个等价关系,若<x,y>属于R,称x等价与y,记x~y.
x的等价类则是A中所有与x等价元素的集合
R中所有等价类作为元素的集合称为A关于R的商集。记作A/R
—————————————————————————————————————————————————————————
偏序关系
原文:https://www.cnblogs.com/liuzhaojun/p/11559347.html