吴恩达机器学习入门笔记5-正则化

5 正则化

给参数增加惩罚项，达到简化假设函数，降低过拟合的目的

5.1 正则化线性回归

5.1.1 正则化代价函数

\[ J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]\tag{5.1} \]

右边加的项称为正则化项，\(\lambda\)称为正则化参数，有两个目标

1. 更好地拟合训练集
2. 保证1的同时尽量减小参数，保持假设模型简单避免出现过拟合情况

• 一般约定不对\(\theta_0\)进行正则化
• 若\(\lambda\)设置过大，参数会接近于0，导致假设函数只有\(\theta_0\)项，即假设函数是一条水平直线，因此需要选择一个合适的正则化参数

5.1.2 正则化梯度下降

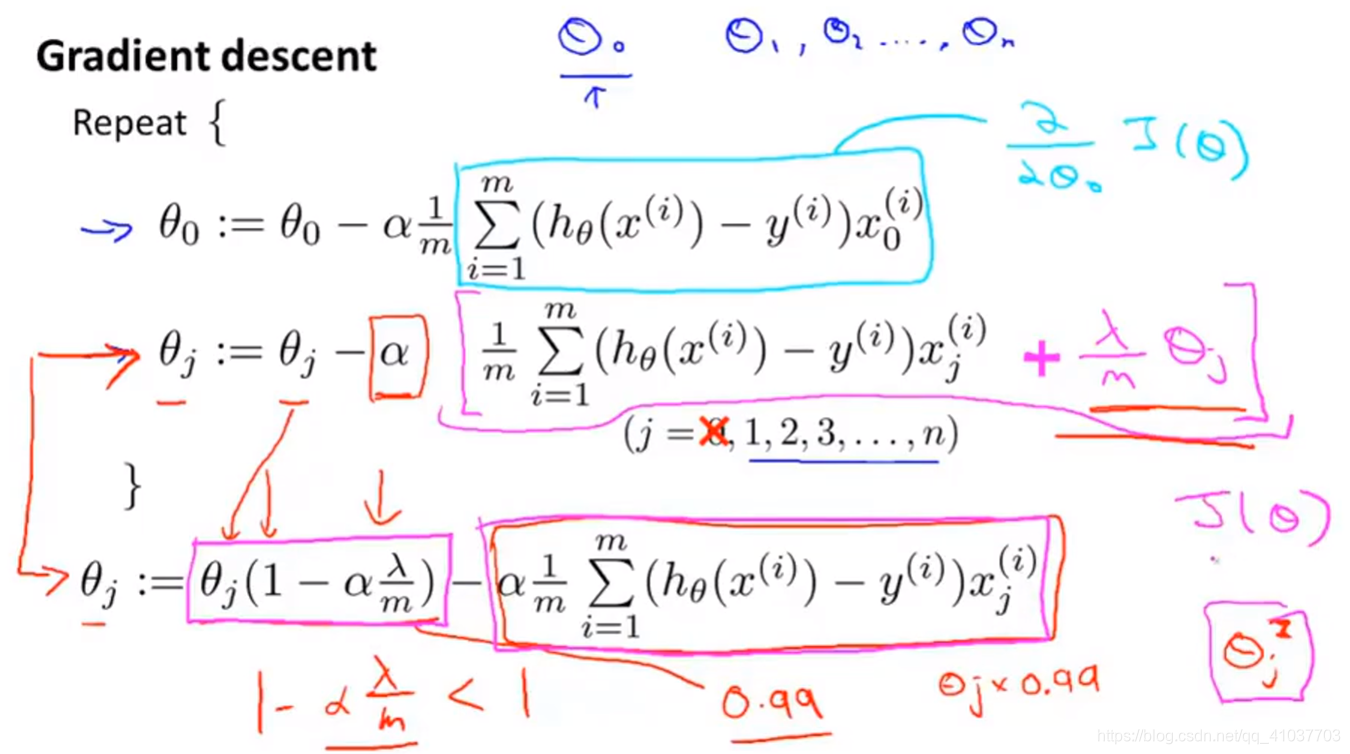
学习率\(\alpha\)很小，样本量m很大，因此正则化即每次将参数向0方向缩小一点

5.1.3 正则化正规方程

\[ \theta=\left(X^{T} X+\lambda\left[\begin{array}{cccc}{0} \\ {} & {1} \\ {} & {} & {1} \\ {} & {} & {} & {\ddots} \\ {} & {} & {} & {1}\end{array}\right]\right)^{-1} X^{T} y\tag{5.2} \]

其中加入的矩阵为(n+1)×(n+1)维

• 如果样本量m小于特征变量个数n，则\(X^TX\)不可逆，为奇异矩阵，但只要\(\lambda>0\)，可确保矩阵和非奇异

5.2 正则化逻辑回归

5.2.1 正则化代价函数

\[ \begin{aligned} J(\theta)=-[\frac{1}{m}\sum_{i=1}^{m} y^{(i)} \log h_{\theta}(x^{(i)})+(1-y^{(i)}) \log (1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2 \end{aligned}\tag{5.3} \]

• 计算后一项记得从j=1开始，因为不正则化\(\theta_0\)

5.2.2 正则化梯度下降

5.2.3 正则化高级算法

5.3 正则化与偏差方差的关系

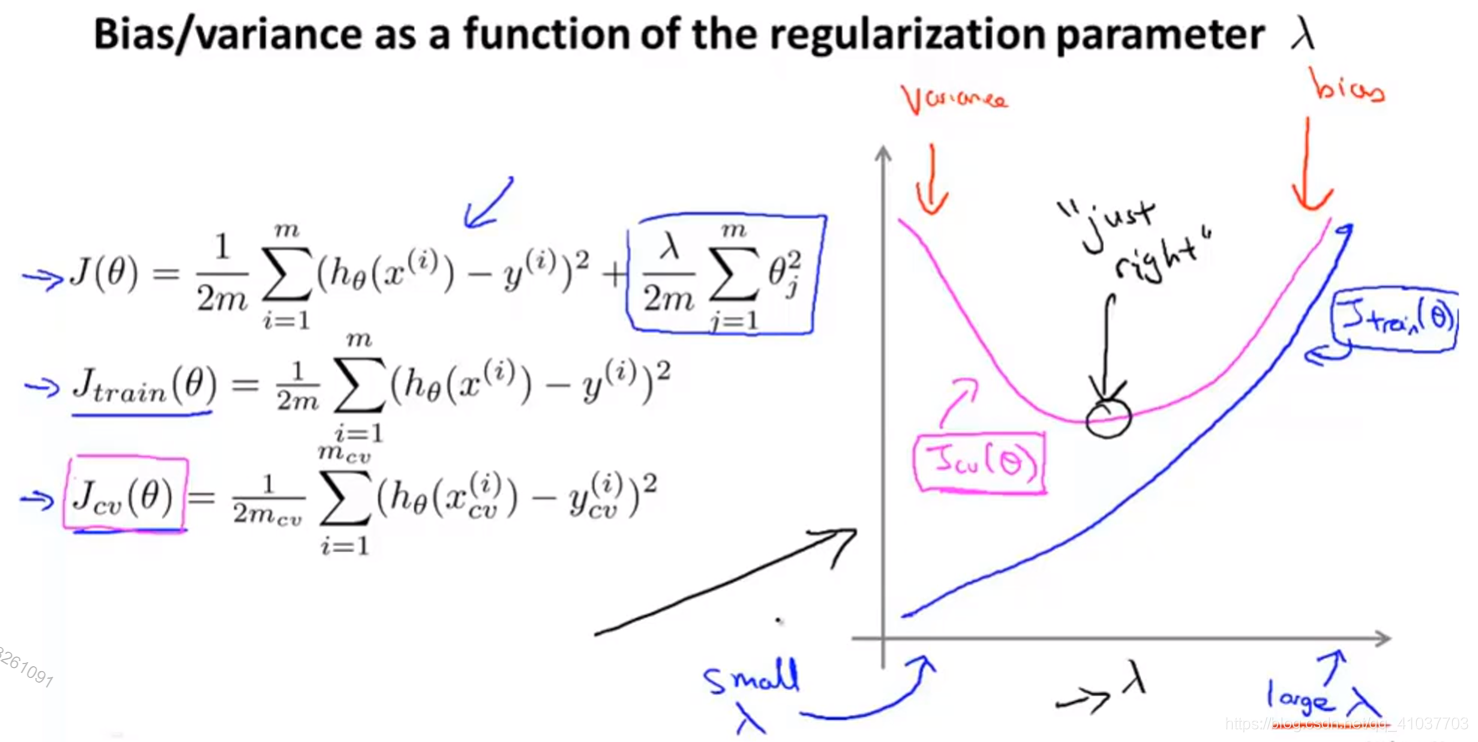
\(\lambda\)越大，训练集和验证集的偏差越大，\(\lambda\)越小，训练集的误差越小，验证集的方差越大

吴恩达机器学习入门笔记5-正则化

原文：https://www.cnblogs.com/jestland/p/11548491.html