论文阅读——《动态规划》 作者 方奇

关健字：阶段  状态  决策  函数递推式

动态规划：指一种解决多阶段决策最优化问题的方法，动态指在每一个可能出现的情况中做出决策后引起状态转移。

例题1：现有一张地图，各结点代表城市，两结点间连线代表道路，线上数字表示城市间的距离。如图1所示，试找出从结点1到结点10的最短路径。

1.  本题可以直接使用穷举法，将节点1——10的所有路线都走一边，记录一个最小值
2. 仔细看一波图，发现可以将图分为五层：1，23，456，789，10（每层的点不相连，除了第一层和第五层，其他层都可以且只能到达上和下层）

• 对分层进行分析的话，可以看出中间三层每一层上每个节点都可以作为上一层的重点和这一层的起点。
• 这时候问题就变成了：求出由第一层到第五层的最小距离。又因为每一层都是相对独立的，到每一层的某个节点的决策，只依赖于上一层的计算结果，这样就成功的将问题分为了多个阶段
• 假设目前处于第三层，那么第一层到4的距离是5，到5的距离是6，到6的距离是5，下面要求到第4层8的距离min（6+5，5+5）=10
• 这样就大大减少了计算量。

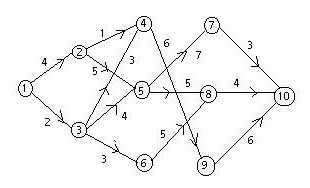
动态规划中的一些术语：

1. 阶段：将问题分为几个相互联系的有顺序的几个环节，这些环节称作阶段。
2. 状态：某个阶段的起始位置。（上面图1中的点2，3就是第二个阶段的状态）
3. 决策：从某阶段的某个状态演变到下一个阶段的某个状态的选择
4. 策略：从开始到结束的每段决策组成的序列称为策略
5. 状态转移方程：决策的运行公式，可使得前一阶段的某状态照此变为下一阶段的某个状态。
6. 目标函数与最优化概念：目标函数是衡量多阶段决策过程优劣的准则。最优化概念是在一定条件下找到一个途径，经过按题目具体性质所确定的运算以后，使全过程的总效益达到最优。

动态规划的使用前提：

1. 满足最优化原理:即全局最优可以由每一个状态下的最优推导得出。
2. 无后效性: 前面做出的决策不会影响后面决策，过去的步骤只能通过现在的状态影响未来发展。当前决策与后续决策无关。状态出现在策略的任何一个位置都可实施相同策略。

动态规划的计算方法：

1. 分析题意，判断是否满足上述的两个条件
2. 尝试确定状态，阶段，约束和边界条件
3. 推导状态转移方程

例题2：

 排队买票

    问题描述：一场演唱会即将举行。现有N（O〈N〈=200）个歌迷排队买票，一个人买一张，而售票处规定，一个人每次最多只能买两张票。假设第I位歌迷买一张票需要时间Ti（1〈=I〈=n），队伍中相邻的两位歌迷（第j个人和第j+1个人）也可以由其中一个人买两张票，而另一位就可以不用排队了，则这两位歌迷买两张票的时间变为Rj，假如Rj〈Tj+Tj+1，则这样做就可以缩短后面歌迷等待的时间，加快整个售票的进程。现给出N，Tj和Rj，求使每个人都买到票的最短时间和方法。

先判断是否满足上述条件：当所有人买票最快时，显然n-1个人买票一定也最快，n-2个人也最快。并且前面的人怎么买票与后面的人怎么买票无关

那么阶段和状态也很好划分，阶段就是买票的先后顺序，状态就是第i个人买票。，那么记s[i]为第i个人买完票之后所花的最短时间

则这个人可以自己买票，也可以和自己前面的人一起买，s[i]=min(s[i-1]+Ti,s[i-2],Ri-1);

这样从前往后进行遍历就可以求出时间，初始化s[1]=T1;

 当然也可以倒推 记dp[i]为倒着买票到第i个人，则有dp[i]=min(dp[i-1]+Ti,dp[i-2]+R(i+1));自己买或者和前面的人一起买

那么初始状态dp[n]=Tn,dp[n+1]=0,其余全为998244353（INF）

例题3：

给你一张图，求A到J的最短路

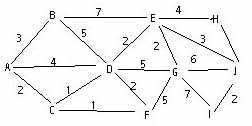
你看这张图，它又长又宽！

1. 刚才的套路行不通了，这张图没有办法分出层次（点EGIJH了解一下）
2. 但是这肯定还是能DP的，只不过状态要改一下。
3. 　　

论文阅读——《动态规划》 作者 方奇

原文：https://www.cnblogs.com/XLINYIN/p/11504101.html