树的介绍
(1)每个结点有零个或多个子结点
(2)没有父节点的结点称为根节点
(3)每一个非根结点有且只有一个父节点
(4)除了根结点外,每个子结点可以分为多个不相交的子树
子节点:子节点是父节点的下一层节点。
- 节点的层次:从根节点开始,根节点为第一层,根的子节点为第二层,以此类推
- 兄弟节点:拥有共同父节点的节点互称为兄弟节点
度
树的深度(Depth)或高度是树中结点的最大层次。
二叉树
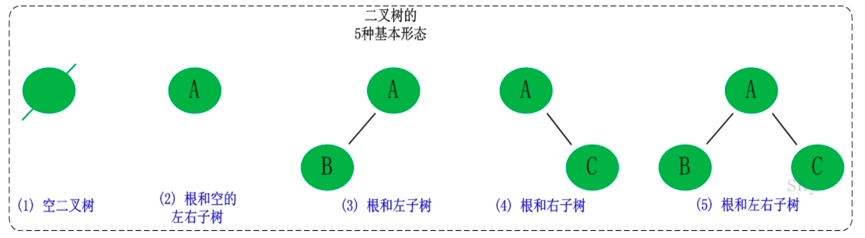
为什么需要平衡二叉树?
为了避免这种情况的发生,我们希望可以有一种算法,将我们的不平衡的二叉排序树转化为平衡二叉排序树。这样就可以让我们的二叉排序树结构最优化。
平衡因子

平衡二叉树旋转
LL型

LR型
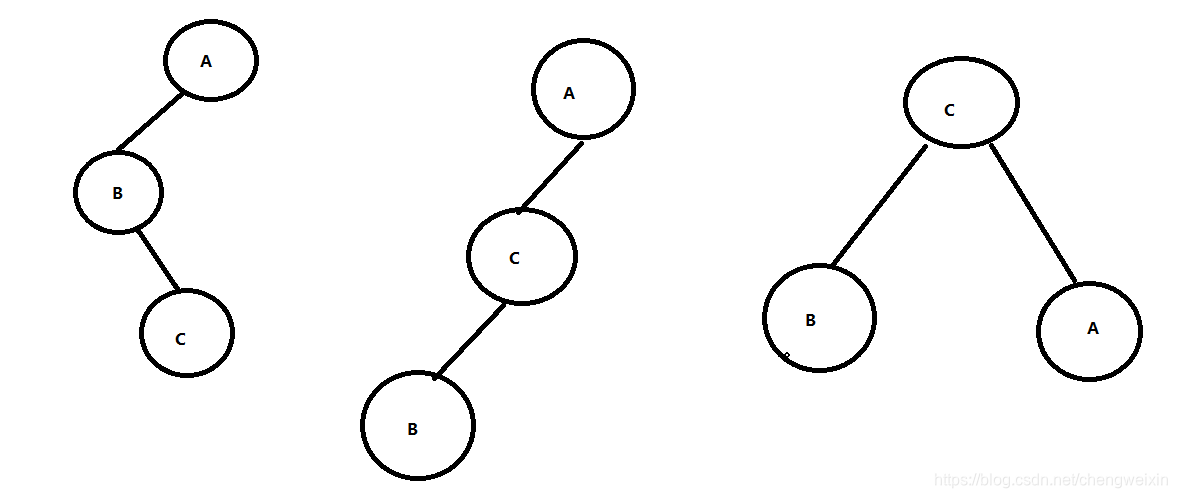
RR型
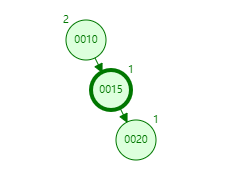
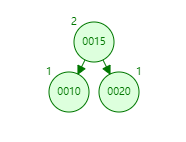
RL型
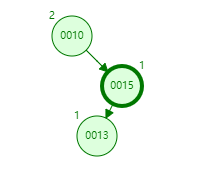

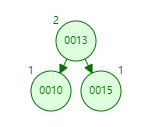
情况一
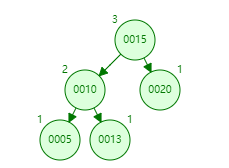
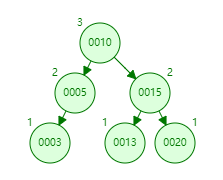
情况二
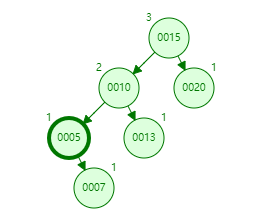
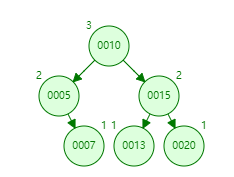
情况三
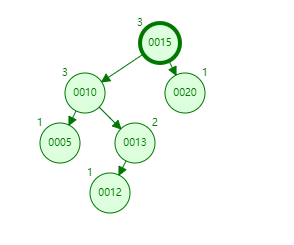
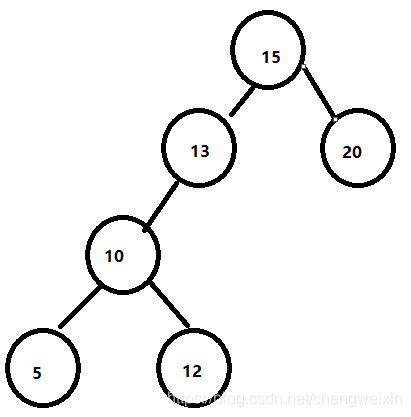
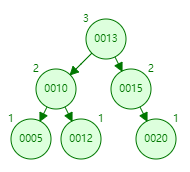
情况四
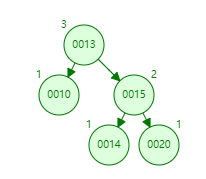
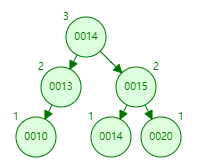
添加节点14
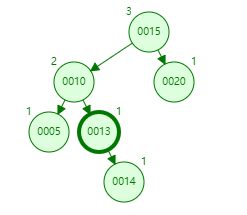
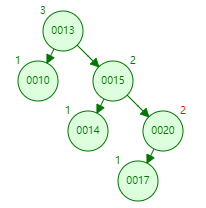
先旋转程LL型,第一次旋转
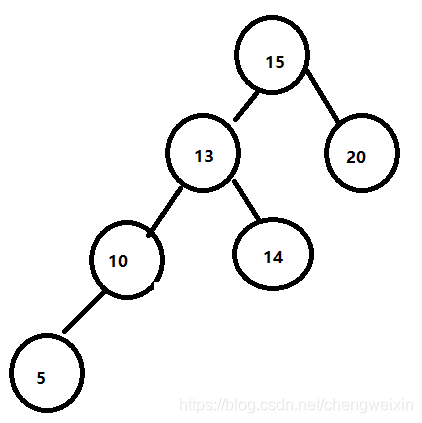
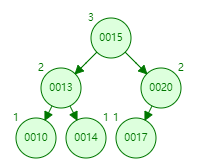
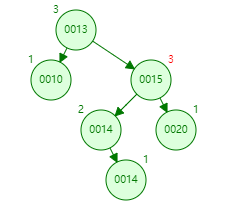
第二次,基于LL型,进行调整
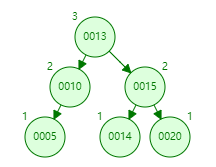
其他在右边添加节点,就是基于上几种情况的镜像调整,先调整成RR型,然后基于RR型二次调整成平衡状态。

红黑树介绍
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构。
它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的 “红黑树” 。
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点(NIL节点,空节点)是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
左旋和右旋
插入操作:
在对红黑树进行插入操作时,我们一般总是插入红色的节点,因为这样可以在插入过程中尽量避免对树的调整。 那么,我们插入一个节点后,可能会使原树的哪些性质改变列?
如果插入的节点是根节点,性质2会被破坏,如果插入节点的父节点是红色,则会破坏性质4。 因此,总而言之,插入一个红色节点只会破坏性质2或性质4。
我们的恢复策略很简单,插入修复具体操作情况:
原树是空树,此情况只会违反性质2。
对策:直接把此节点涂为黑色。
情况2:插入的节点的父节点是黑色。
此不会违反性质2和性质4,红黑树没有被破坏。
对策:什么也不做。
情况3:当前节点的父节点是红色且祖父节点的另一个子节点(叔叔节点)是红色。
此时父节点的父节点一定存在,否则插入前就已不是红黑树。与此同时,又分为父节点是祖父节点的左子还是右子,对于对称性,我们只要解开一个方向就可以了。 在此,我们只考虑父节点为祖父左子的情况。 同时,还可以分为当前节点是其父节点的左子还是右子,但是处理方式是一样的。我们将此归为同一类。
对策:将当前节点的父节点和叔叔节点涂黑,祖父节点涂红,把当前节点指向祖父节点,从新的当前节点重新开始算法。
针对情况3,变化前[当前节点为4节点]:
? 变化后:
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如下图所示,变化前[当前节点为7节点]:
? 变化后:
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如下图所示[当前节点为2节点]
? 变化后:
总结:
经过上面情况3、情况4、情况5等3种插入修复情况的操作示意图,自会发现,后面的情况4、情况5都是针对情况3插入节点4以后,进行的一系列插入修复情况操作,不过,指向当前节点N指针一直在变化。所以,你可以认为:整个下来,情况3、4、5就是一个完整的插入修复情况的操作流程。

关注公众号-免费获取【JAVA核心知识点】!!

原文:https://www.cnblogs.com/yidiankt/p/11458040.html