归并排序

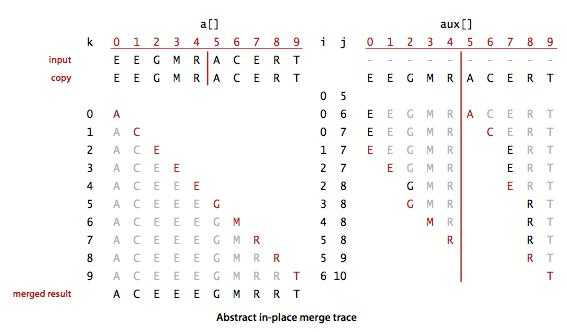
将两个有序的数组归并成一个更大的有序数组。

原地归并的抽象方法

public static void merge(Comparable a[], int lo, int mid, int hi) {
    int i = lo, j = mid + 1;//两个待归半边并的头
    //将代归并的元素放入到aux中
    for (int k = lo; k <= hi; k++) {
        aux[k] = a[k];
    }
    for (int k = lo; k <= hi; k++) {
        if (i > mid) {//左半边用尽
            //取右半边的元素
            a[k] = aux[j++];
        } else if (j > hi) {//右半边用尽
            //取左半边的元素
            a[k] = aux[i++];
        } else if (less(aux[j], aux[i])) {
            a[k] = aux[j++];
        } else {
            a[k] = aux[i++];
        }
    }
}

该方法先将元素复制到 aux[] 中，然后再归并到 a[] 中。方法再归并时（第二个 for 循环）进行了 4 个条件判断，分别是：

• 左半边用尽（取右半边的元素）
• 右半边用尽（取左半边的元素）
• 右半边的当前元素小于左半边的当前元素（取右半边的元素）
• 右半边的当前元素大于等于左边的当前元素（取左半边的元素）
  

自顶向下递归

分治思想

static Comparable[] aux;
public static void sort(Comparable a[]) {
    aux = new Comparable[a.length];
    sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) {//当切分到左右只有一个元素时，左右部分有序开始第一次归并
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(a, lo, mid);
    sort(a, mid + 1, hi);
    merge(a, lo, mid, hi);
}

自底向上

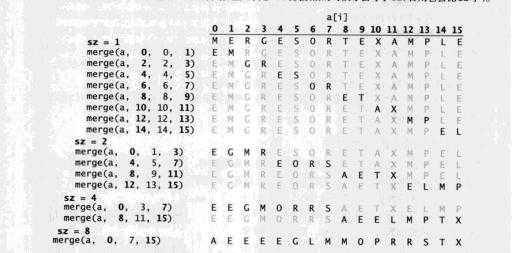
    static Comparable[] aux;
    public static void sort01(Comparable a[]) {
        int N = a.length;
        aux = new Comparable[N];
        for (int sz = 1; sz < N; sz = sz + sz) {
            for (int lo = 0; lo < N - sz; lo = sz + sz + lo) {
                merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
            }
        }
    }

特点

-归并排序是一种稳定的排序。
-归并排序需要O(n)的辅助空间，它不是就地排序。

归并排序

原文：https://www.cnblogs.com/aiguozou/p/11407088.html