拉格朗日插值法

     在具体的工作应用中，可能需要我们描述某一个曲线，但是该曲线又不是普通的抛物线等简单的可易描述图形。实际情况可能如下：已知n+1个点的坐标，某图形过这几个点，求该图形的方程，或者在其他未知点的位置坐标。此时，我们可通过拉格朗日插值来求出这个曲线。

　　场景中已知n+1个点坐标分别为(x₀,y₀)，(x₁,y₁)，... ，(x_n,y_n)，拉格朗日插值法格式为：

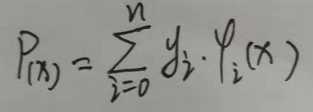
　　上式中的y_i指的是x_i时的y值，φ_i(x)指的是拉格朗日基本多项式（又称插值基函数）。

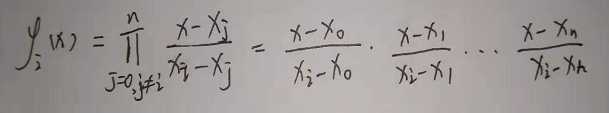
　　例子：

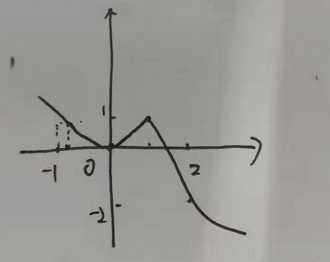
 　　如上图所示，该图形过四个点，f(-1) = 1, f(0) = 0, f(1) = 1, f(2) = -2

　　我们先求其各个点的拉格朗日基本多项式。　　

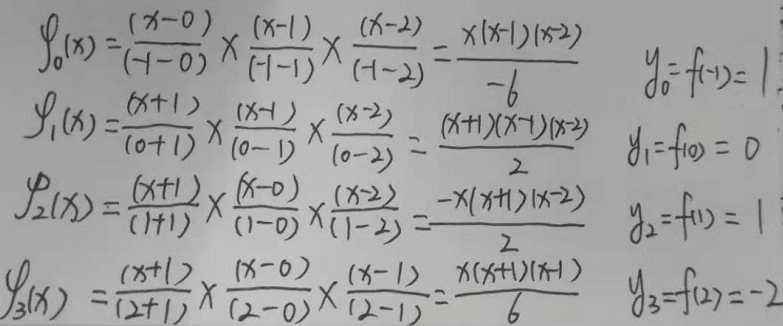
综上所述，根据拉格朗日插值法，计算曲线方程

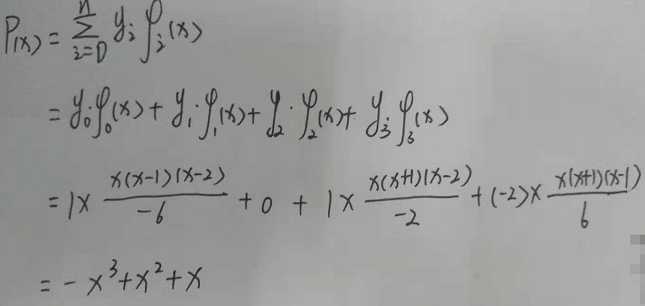
　　总的来说，拉格朗日插值法相对简单，计算过程易于理解，但是每增加一个点，曲线方程就需要改变，没有统一的方程。这也是他的局限性。

拉格朗日插值法

原文：https://www.cnblogs.com/strangemonkey/p/11391396.html