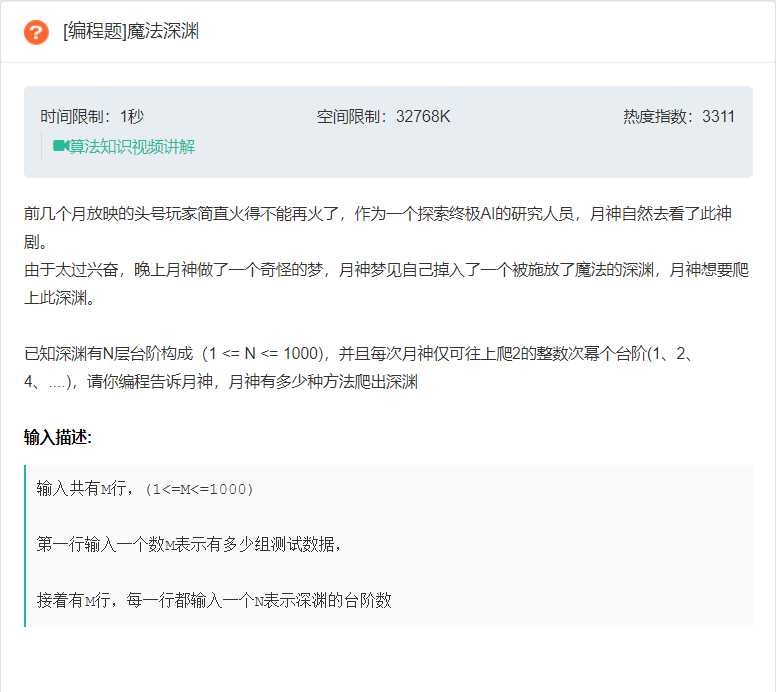
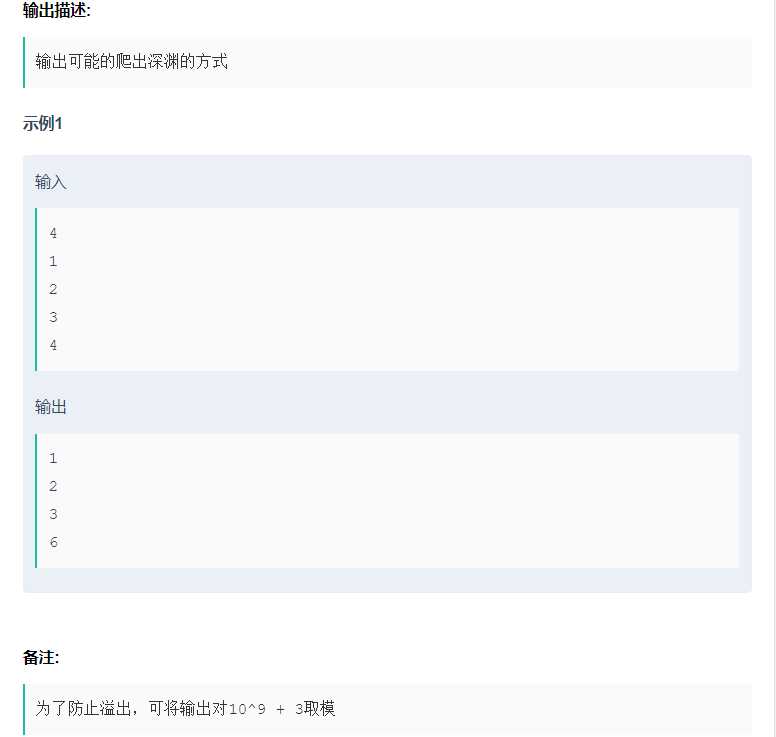
分析:递归或者dp,爬楼梯很老的一道题目
当前台阶方法数 = 所有一次可到达当前台阶方法数的和
最初的题目是只能上1、2、3个台阶所以dp[i]+=dp[i-1]+dp[i-2]+dp[i-3];
这个是1,2,4,8,16,32,就是2^n方,也就是只要t=i-2^n>=0,dp[i]+=dp[i-t]
dp的ac代码如下:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1000+5;
int dp[maxn];
int main()
{
int N,n;
cin>>n;
while(n--){
cin>>N;
memset(dp,0,sizeof(dp));
dp[0]=dp[1]=1;
dp[2]=2;
dp[3]=3;
for(int i=4;i<=N;i++){
for(int j=0;j<i;j++){
int tmp=i-pow(2,j);
if(tmp>=0){
dp[i]+=dp[tmp];
dp[i]=dp[i]%1000000003;
}
else break;
}
}
cout<<dp[N]<<endl;
}
return 0;
}
用递归只能过50%的数据
#include <bits/stdc++.h>
using namespace std;
int solution(int N){
int s=0;
if(N==1||N==0) return 1;
if(N==2) return 2;
if(N==3) return 3;
for(int i=0;pow(2,i)<=N;i++){
s+=solution(N-pow(2,i));
}
return s;
}
int main()
{
int N,n;
cin>>n;
while(n--){
cin>>N;
cout<<solution(N)<<endl;
}
return 0;
}
原文:https://www.cnblogs.com/cstdio1/p/11382192.html