▎排列
?『引入』
思考一个问题：
你的眼前现在有三个人：gzr、lsh、hza，如何排列他们的位置呢？
显然，有这样的排法：
gzr、lsh、hza
gzr、hza、lsh
hza、lsh、gzr
hza、gzr、lsh
lsh、gzr、hza
lsh、hza、gzr
一共是六种。
?『定义』
这不就是排个顺序吗？相信定义就不需要拿出来讲了。
但是唯一要注意一点：排列是关心顺序的。
?『n中选n个求解』
那么我们在n个人中进行排列的方案数有多少种呢？
显然，第一个人有n种方案;
第二个人有n-1种方案;
第三个人有n-2种方案;
……
第n个人有1种方案;
按照乘法原理，总的方案数就是n*(n-1)*(n-2)*…*2*1。
发现了什么？这岂不是 n！ 。
?『n中选m个求解』
依旧是上面的思路，只不过不是n！了。
现在我们来思考：n！在这种情况下，被多乘了多少次？
当然有（n-m）！次都是多乘的，所以有n！/（n-m）！个方案。
▎排列数
当n个中取m个的时候，我们可以用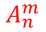
来表示。
比如说5个数排列三个位置就有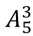
个方案。
▎组合
?『引入』
来思考下面的问题：
有三只小狗，分别是中华田园犬、柴犬、拉布拉多。
但是现在只有两块狗狗零食，那么为了公平起见，一只狗最多只能吃一个，所以只能给两只狗狗吃，剩下的那一只只能下次了。
所以，问题是：分配的方案数有多少种？
这就是组合的问题。
?『定义』
在刚才的问题中，仍然是上面的选择方案数问题，但是却不太一样了。
由于狗狗吃了就是吃了，不会在意顺序，而刚才的排列是在意顺序的。
所以，组合和排列不同的地方就是是否关心顺序是怎样的。
?『求解』
对比刚才的排列，如何快速求出组合的方案数呢？
不难发现同一种组合方式被当作排列一定会算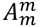
，所以就只要在排列的结果上除以
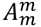就可以了。
所以公式就是：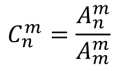
。
▎组合数
?『表示』
刚才的那个C的符号就是组合的符号，和排列的用法一样。
也就是说将n中选m个的排列方案数记做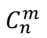
。
?『通项公式』
现在不思考前n-1个数是怎么选的，只关心第n个数。
显然，情况就两种，要么被选，要么不被选。
被选上一定是从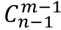
转移来的，不被选上一定是从
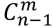转移来的。
所以按照加法原理，通项公式就是这样的：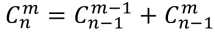
。
原文：https://www.cnblogs.com/TFLS-gzr/p/11336424.html