算是一道比较综合的数论题了吧！用到了欧拉定理，中国剩余定理，卢卡斯这些。
但整道题还是很简单的。
（图片摘自洛谷博客）
题目大意是求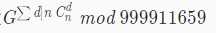
因为指数太大但它是个质数，我们考虑用欧拉定理的推论得到
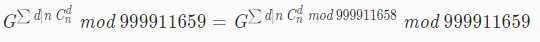
因为与组合数有关，我们会想到用卢卡斯定理，但是999911658这个模数太大（好像卢卡斯模数是可以做1e5级别的）而且不是质数，不可以直接卢卡斯
我们把999911658拆成2*3*4679*35617四个质数，对于每一个质数计算出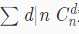
，结果记为a1,a2,a3,a4
最后用中国剩余定理合并得到x
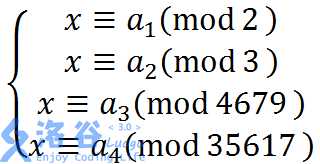
#include<bits/stdc++.h> #define LL long long #define mod 999911658 using namespace std; int read() { int x=0,f=1;char s=getchar(); while(s<‘0‘||s>‘9‘){if(s==‘-‘)f=-1;s=getchar();} while(s>=‘0‘&&s<=‘9‘){x=x*10+s-‘0‘;s=getchar();} return x*f; } int b[]={0,2,3,4679,35617}; LL fac[36000],invfac[36000],a[5]; LL quick(LL a,LL x,LL p) { LL ans=1; while(x) { if(x&1)ans=ans*a%p; a=a*a%p;x>>=1; } return ans%p; } void init(int p) { memset(invfac,0,sizeof(invfac)); fac[0]=1; for(int i=1;i<=p;++i)fac[i]=fac[i-1]*i%p; invfac[p]=quick(fac[p],p-2,p); invfac[p-1]=quick(fac[p-1],p-2,p);//注意不要从fac[p]开始，因为这样推一定是0，mod的是p的嘛 for(int i=p-1;i>=1;--i)invfac[i-1]=invfac[i]*i%p; } LL lucas(int n,int m,int p) { if(n<m)return 0; if(n<p&&m<p) return fac[n]*invfac[m]%p*invfac[n-m]%p; return lucas(n/p,m/p,p)*lucas(n%p,m%p,p)%p; } LL res=0; void CRT() { for(int i=1;i<=4;++i) res=(res+a[i]*(mod/b[i])%mod*quick(mod/b[i],b[i]-2,b[i])%mod)%mod; } int main() { int n=read(),g=read(); if(g%(mod+1)==0) { printf("0\n"); return 0; } for(int k=1;k<=4;++k) { init(b[k]); for(int i=1;i*i<=n;++i) { if(n%i)continue; a[k]=(a[k]+lucas(n,i,b[k]))%b[k]; if(i*i!=n)a[k]=(a[k]+lucas(n,n/i,b[k]))%b[k]; } } CRT(); printf("%lld\n",quick(g,res,mod+1)); }
原文：https://www.cnblogs.com/yyys-/p/11295540.html
