位运算:
负数在计算机内是用补码来表示的。即将数转化为二进制以后,再取反加1.
与运算:and. &
或运算:or. |
异或运算:xor. ^
非运算:not. ~
左移:将一个数字往左移动一位,相当于将该数字乘以2。
右移:将一个数字往右移动一位,相当于将该数字除以2。
位运算技巧:
一,用于消除x的最后一位
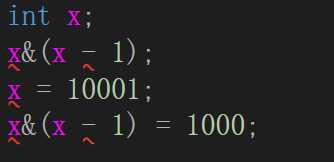
1.1 在O(1)的时间检测整数N是否为2的幂
思路解析:如果N是2的次幂
应该满足两个条件:
1.N>0
2.N的二进制表示中只有一个1,用N&(N-1)将消去唯一的一个1
因此当N&(N-1)=0时,该数为2的幂
1.2 计算在一个32位的整数的二进制中有多少个1
思路解析:循环用X&(X-1)消去最后一个1,当最后一个数不为1时,X&(X-1)==X;循环计数即可
1.3 将整数A转化为整数B,需要改变几位
思路解析:利用异或操作,将A,B整数二进制不同的位用1标识出来,就变成了统计一个整数二进制表示中有多少个1的问题。
二,使用二进制进行子集枚举
应用。给定一个含有不同整数的集合。返回其所有子集。
如果S={1,2,3}。则答案有:{{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}。
思路:使用第i位表示1/0,表示第i位元素取或者不取。
题目:只出现一次的数字
题目描述:给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
要求:时间复杂度不超过O(n),空间复杂为O(1)
【容器vector的简单用法:
vector是向量类型,可以容纳许多种类型的数据,比如整数等。
(1)vector的初始化:
vector<int> a(10) ; 定义了一个类型为整形的含有10各元素的向量。
vector<int> a(10,1); 定义了一个类型为整形的含有10各元素的向量,且每个元素的初始值为1。
vector<int> a(b); 用b向量来创建a向量
vector<int> a(b.begin(),b.begin+3); 定义了a值为b中第0到第2元素的值。
int b[7]={1,2,3,6,7,8,9};
vector<int> a(b,b+7);从数组中获得初值
(2)常用操作
vector<int> a;
a.size();返回向量a的大小】
解法:
相同的两个数经过异或操作“^”以后为0,0与其他任何数进行异或操作之后仍然为其他数。
?
原文:https://www.cnblogs.com/yaggy/p/11294796.html