贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。
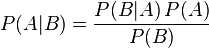
P(A)是 A 的先验概率,之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率,也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率,也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率,也作标淮化常量(normalizing constant)。
推导
可以从条件概率的定义推导出贝叶斯定理。
根据条件概率的定义,在事件 B 发生的条件下事件 A 发生的概率为:
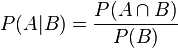
同样地,在事件 A 发生的条件下事件 B 发生的概率为:
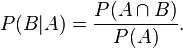
结合这两个方程式,我们可以得到:
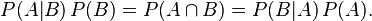
这个引理有时称作概率乘法规则。上式两边同除以 P(A),若P(A)是非零的,我们可以得到贝叶斯定理:
原文:https://www.cnblogs.com/wodeboke-y/p/11266356.html