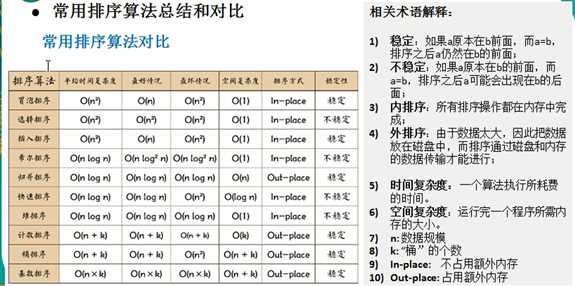
排序算法一般分别是冒泡排序、快速排序、直接插入排序、希尔排序、简单选择排序、堆排序、归并排序和基数排序,如果按原理划分,冒泡排序和快速排序都属于交换排序,直接插入排序和希尔排序属于插入排序,而简单选择排序和堆排序属于选择排序。
扫描所有元素,将最小的与第一位交换位置,再扫描除第一位以外最小的与第二位交换位置。

//选择排序 public static void selectSort(int[] arr) { //在推导的过程,我们发现了规律,因此,可以使用for来解决 //选择排序时间复杂度是 O(n^2) for (int i = 0; i < arr.length - 1; i++) { int minIndex = i; int min = arr[i]; for (int j = i + 1; j < arr.length; j++) { if (min > arr[j]) { // 说明假定的最小值,并不是最小 min = arr[j]; // 重置min minIndex = j; // 重置minIndex } } // 将最小值,放在arr[0], 即交换 if (minIndex != i) { arr[minIndex] = arr[i]; arr[i] = min; } //System.out.println("第"+(i+1)+"轮后~~"); //System.out.println(Arrays.toString(arr));// 1, 34, 119, 101 } }
对最前面两个元素进行排序,将第三个元素插入到合适位置,插入过程种要求,其他元素后移,为新插入元素腾出位置。
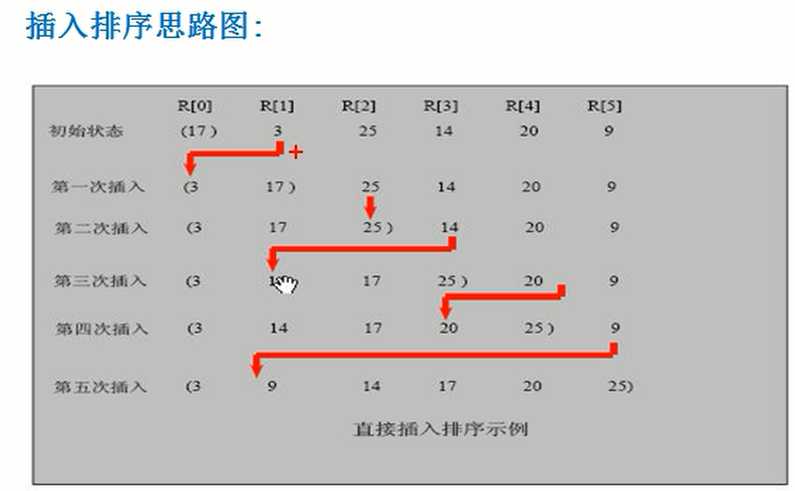
//插入排序 public static void insertSort(int[] arr) { int insertVal = 0; int insertIndex = 0; //使用for循环来把代码简化 for(int i = 1; i < arr.length; i++) { //定义待插入的数 insertVal = arr[i]; insertIndex = i - 1; // 即arr[1]的前面这个数的下标 // 给insertVal 找到插入的位置 // 说明 // 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界 // 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置 // 3. 就需要将 arr[insertIndex] 后移 while (insertIndex >= 0 && insertVal < arr[insertIndex]) { arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex] insertIndex--; } // 当退出while循环时,说明插入的位置找到, insertIndex + 1 // 举例:理解不了,我们一会 debug //这里我们判断是否需要赋值 if(insertIndex + 1 != i) { arr[insertIndex + 1] = insertVal; } //System.out.println("第"+i+"轮插入"); //System.out.println(Arrays.toString(arr)); } }
冒泡排序算法的算法过程如下:
①. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
②. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
③. 针对所有的元素重复以上的步骤,除了最后一个。
④. 持续每次对越来越少的元素重复上面的步骤①~③,直到没有任何一对数字需要比较。
如果有一趟排序下来没交换,则代表已经有序。
// 将前面额冒泡排序算法,封装成一个方法 public static void bubbleSort(int[] arr) { // 冒泡排序 的时间复杂度 O(n^2), 自己写出 int temp = 0; // 临时变量 boolean flag = false; // 标识变量,表示是否进行过交换 for (int i = 0; i < arr.length - 1; i++) { for (int j = 0; j < arr.length - 1 - i; j++) { // 如果前面的数比后面的数大,则交换 if (arr[j] > arr[j + 1]) { flag = true; temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } //System.out.println("第" + (i + 1) + "趟排序后的数组"); //System.out.println(Arrays.toString(arr)); if (!flag) { // 在一趟排序中,一次交换都没有发生过 break; } else { flag = false; // 重置flag!!!, 进行下次判断 } } }
快速排序(Quicksort)是对冒泡排序的一种改进,借用了分治的思想,由C. A. R. Hoare在1962年提出。
选择表中的一个元素当作划分元素,对表进行划分,小于划分元素的所有元素都放到划分元素左侧,大于划分元素的所有元素都放到元素右侧,最后再递归地对两个子划分段进行排序。
快速排序并不稳定,快速排序每次交换的元素都有可能不是相邻的, 因此它有可能打破原来值为相同的元素之间的顺序。
public static void quickSort(int a[],int left,int right ){ if(left>=right) return; int pivot=a[left]; int i=left; int j=right; //如果左右指针碰头就代表这一轮迭代结束 while (i!=j){ //先从右边开始,找小于pivot点的数字 //因此,循环的条件是如果大于pivot就继续查找 //小于pivot就停止 while(a[j]>=pivot&&i<j){ //count++; j--; } //后从左边开始,找大于pivot的数字 //因此,循环的条件是如果是小于pivot就继续查找 //大于pivot就停止 while(a[i]<=pivot&&i<j){ // count++; i++; } if(i<j) { //交换两个数字 int temp = a[j]; a[j] = a[i]; a[i] = temp; } } //基准归位 a[left]=a[i]; a[i]=pivot; quickSort(a,left,i-1); quickSort(a,i+1,right); }
性能分析
(1)时间复杂度分析
快速排序最好情况下的时间复杂度为O(nlog2n),待排序列越接近无序,本算法效率越高。最坏情况下的时间复杂度为O(n2),待排序列越接近有序,本算法效率越低。平均时间复杂度为O(nlog2n)。就平均时间而言,快速排序是所有排序算法中最好的。快速排序的排序趟数与初始序列有关。
(2)空间复杂度分析
本算法空间复杂度为O(log2n)。快速排序是递归进行的,递归需要栈的辅助,因此它需要的辅助空间较多。
开始时将表划分为大致相等的两段,然后对每个字表递归调用自身,直到划分为很多只含一个元素的子表,然后控制返回递归调用结构,算法将从两个递归调用中得到两个有序字段,合并为一个有序表。
比如初始数组:[24,13,26,1,2,27,38,15]
①分成了两个大小相等的子数组:[24,13,26,1] [2,27,38,15]
②再划分成了四个大小相等的子数组:[24,13] [26,1] [2,27] [38,15]
③此时,left < right 还是成立,再分:[24] [13] [26] [1] [2] [27] [38] [15]
此时,有8个小数组,每个数组都可以视为有序的数组了!!!,每个数组中的left == right,从递归中返回(从19行--20行的代码中返回),故开始执行合并(第21行):
merge([24],[13]) 得到 [13,24]
merge([26],[1]) 得到[1,26]
.....
.....
最终得到 有序数组
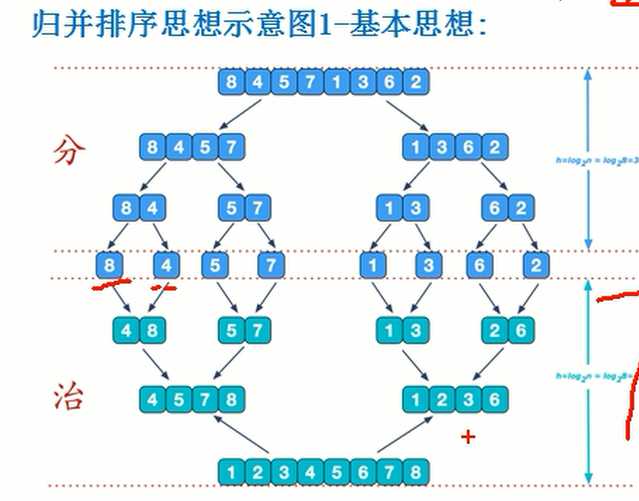
由上图可看出归并排序时间复杂度为n-1 ,为线性增长。
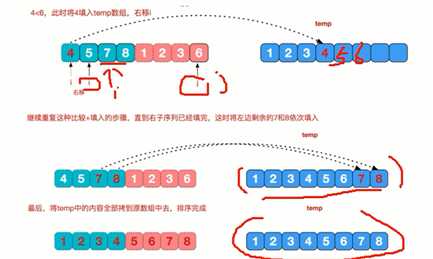
治的过程以倒数第二组为例:
public class MergeSort { public static <T extends Comparable<? super T>> void mergeSort(T[] arr) { T[] tmpArray = (T[]) new Comparable[arr.length]; mergeSort(arr, tmpArray, 0, arr.length - 1); } /** * * @param arr an array of Comparable items * @param tmpArray an array to place the merge result * @param left the left-most index of the array * @param right right-most index of the array */ private static <T extends Comparable<? super T>> void mergeSort(T[] arr, T[] tmpArray, int left, int right) { if (left < right) { int center = (left + right) / 2; mergeSort(arr, tmpArray, left, center); mergeSort(arr, tmpArray, center + 1, right); merge(arr, tmpArray, left, center + 1, right); } } /** * * @param arr an array of Comparable items * @param tmpArray an array to place the merge result * @param leftPos the left-most index of the subarray * @param rightPos the index of the start of the second half * @param rightEnd the right-most index of the subarray */ private static <T extends Comparable<? super T>> void merge(T[] arr, T[] tmpArray, int leftPos, int rightPos, int rightEnd) { int leftEnd = rightPos - 1; int numElements = rightEnd - leftPos + 1; int tmpPos = leftPos;// 只使用tmpArray中某一部分区域 while (leftPos <= leftEnd && rightPos <= rightEnd) { if (arr[leftPos].compareTo(arr[rightPos]) <= 0) tmpArray[tmpPos++] = arr[leftPos++]; else tmpArray[tmpPos++] = arr[rightPos++]; } while (leftPos <= leftEnd) tmpArray[tmpPos++] = arr[leftPos++];// copy rest of left half while (rightPos <= rightEnd) tmpArray[tmpPos++] = arr[rightPos++];// copy rest of right half // copy tmpArray back for (int i = 0; i < numElements; i++, rightEnd--) arr[rightEnd] = tmpArray[rightEnd];//只拷贝当前 merge 的部分数组 /** * 复制了整个数组中的所有元素 for(int i = 0; i < tmpArray.length; i++) arr[i] = tmpArray[i]; */ } //for test purpose public static void main(String[] args) { Integer[] arr = {24,13,26,1,2,27,38,15}; mergeSort(arr); for (Integer i : arr) System.out.print(i + " "); } }
参考 https://blog.csdn.net/flyingsbird/article/details/79533075
原文:https://www.cnblogs.com/dingpeng9055/p/11131194.html