Tarjan无向图的割点和桥(割边)详解&算法笔记&通俗易懂

原文链接

Tarjan无向图的割点和桥(割边)

导言

在掌握这个算法前,咱们有几个先决条件.

• [x] DFS搜索
• [x] DFS序
• [x] 一张纸
• [x] 一支笔
• [x] 认真的大脑(滑稽)

如果您都具备了,那么您就是巨佬了,您就可以轻松解决Tarjan算法了.

初学算法

概念掌握

割点

概念定义什么的,看上去好烦好烦好烦的,怎么办呢?

Acwing小剧场开播了,门票一枚AC币.

现在Acwing推出了一款战略游戏,名为Tarjan无向图的割点和桥.

贪玩Tarjan,介个是泥从未丸过的船新版本.

整个游戏,由\(N\)个岛屿构成,而且有\(M\)条航线联络着这些岛屿.

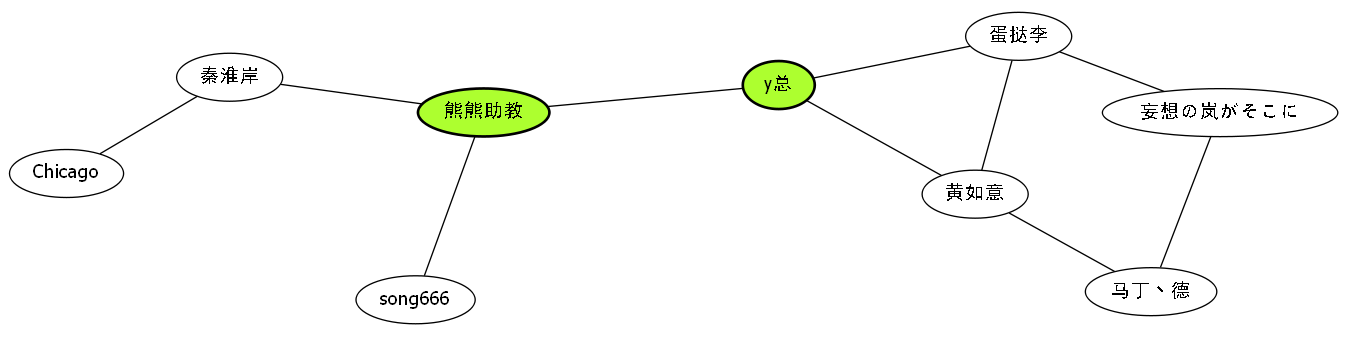
我们发现熊熊助教和y总这两个点非常重要,是整张地图的核心战略要塞.

假如说缺少了任意一个点,我们发现总会有两个岛屿,不能联系了.

因此我们得出了,核心战略要塞,就是交通联络点.

所以这些点要重要中药保护,避免被破坏,

因此我们把这些要重要保护的点,也就是交通联络点,称之为割点.

割边

同样的有核心战略要塞,也就会有黄金水道.

什么是黄金水道呢?

难道是航运量大的航道?

不不不不,这个概念不一样.

如果说黄金水道被破坏了,那么将会有两个和两个以上的岛屿,不能够通航连接了.

比如说,熊熊助教和y总连接的一条航道.

还有熊熊助教和song666连接的航道.

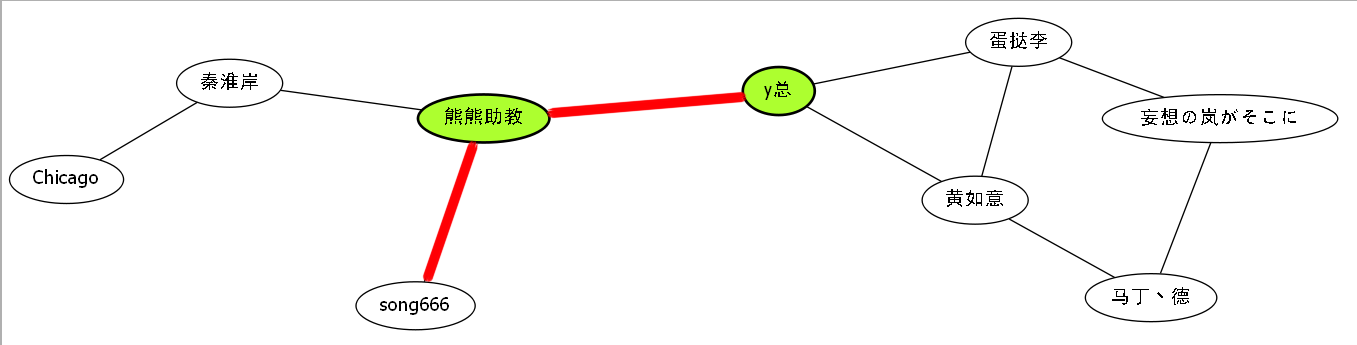
这就是我们的黄金水道,也就是战略航道.

因此我们给这些战略航道定义为桥(割边).

时间戳

其实啊,我们完全可以给这些岛屿们编号.这样便于管理,有利于愉悦身心健康.

因此我们得出了下面这张图片.

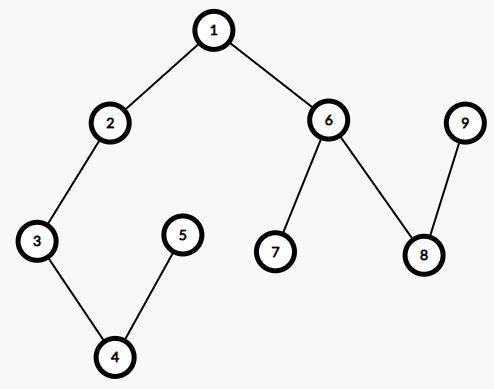
我们发现删除了一些多余的边,然后每个点多了一个学号.

其实我们的学号,就是每一个节点的时间戳.

什么是时间戳,就是每一个点的学号.

但是这个学号是怎么来的呢?总不能是一顿瞎排的吧.

其实这个学号,就是我们的DFS序,刚开始我们任意选择一个点开始,然后一次深度优先搜索,每新搜索到一个点后,就给这个点标记一个学号.

然后来一个gif动画看一看.

因此时间戳的定义我们就知道了.

这就是时间戳的概念,其实就是学号编辑的过程.

追溯值

追溯,追溯,就是寻找一个节点,以他为根,可以抵达的最小学号.

我们设置一个小概念
\[ subtree(x)表示搜索树中以x节点为根的子树节点集合. \]
比如说我们举一个例子.

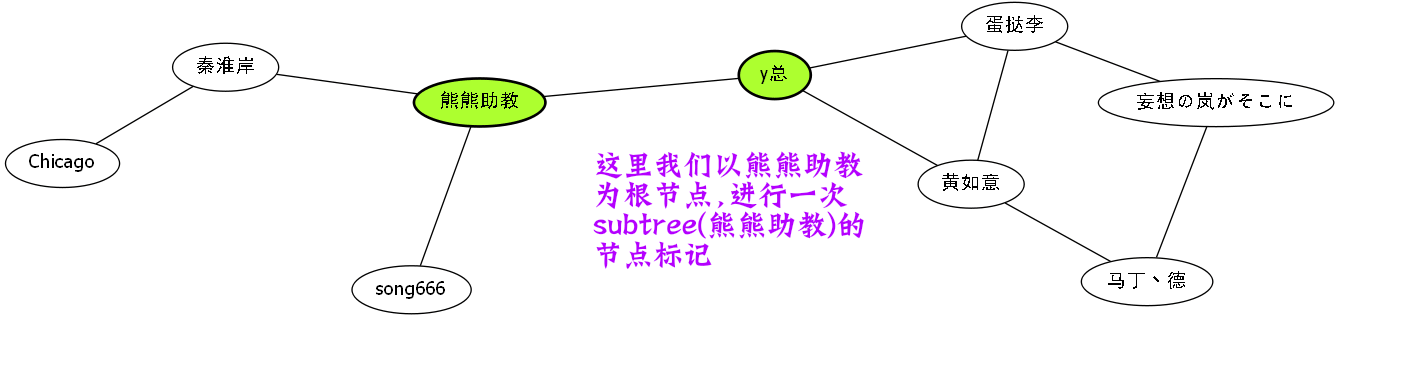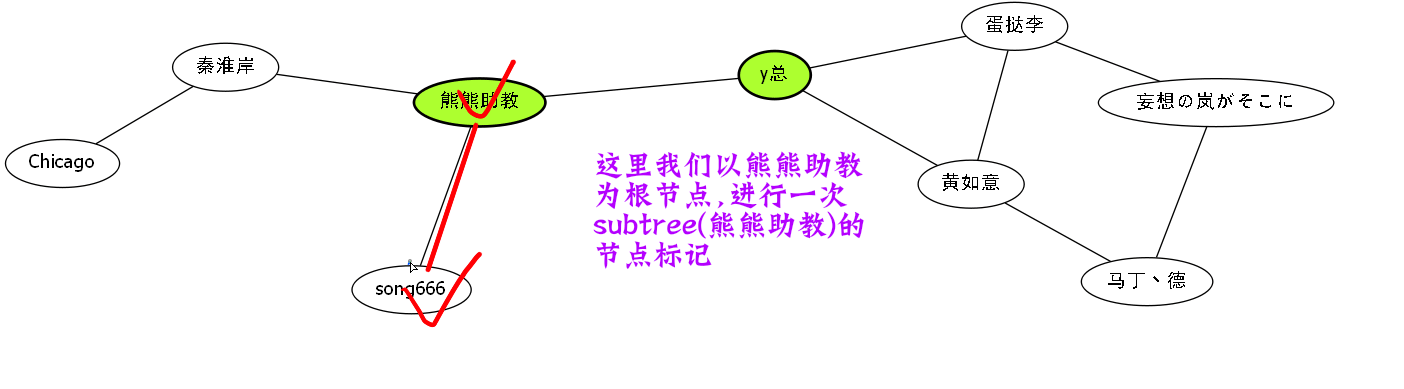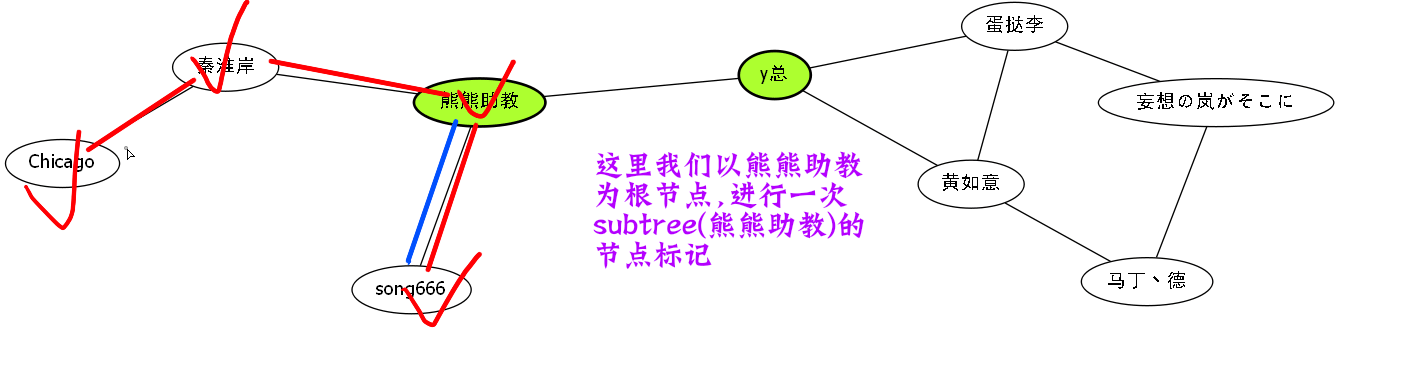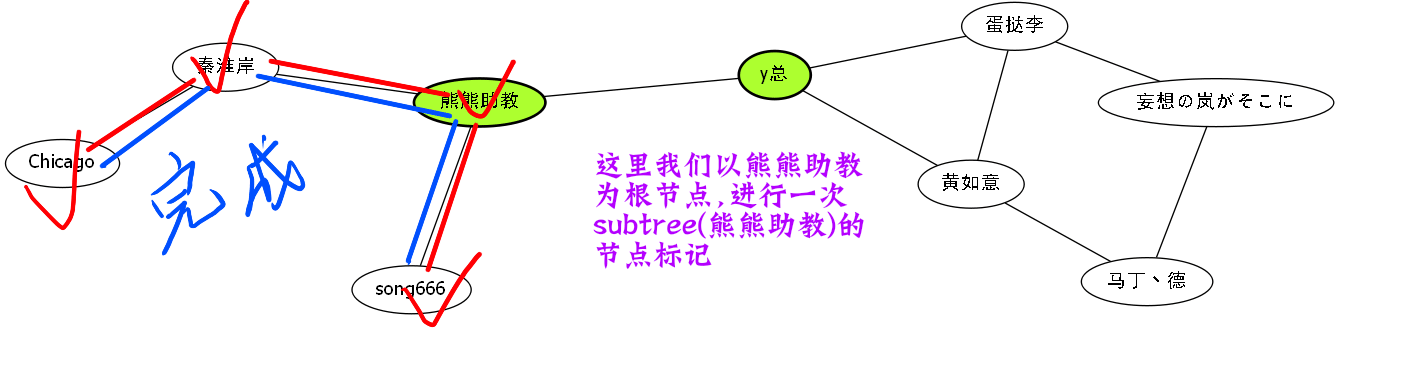
这些红色标记节点,其实也就是熊熊助教的搜索树.

因此我们得出.
\[ subtree(熊熊助教)=(熊熊助教,song666,秦淮岸,Chicago) \]
那么我们设置一下追溯值数组.
\[ low[x]定义为以下节点的时间戳的最小值. \]

1. \(subtree(x)\)中的节点
2. 通过\(1\)条不在搜索树上的边,能够抵达\(subtree(x)\)中的节点.

这个第一条我们上面解释过了,那么第二条怎么解释呢,还是一样,我们再来一个解释gif.

判定法则

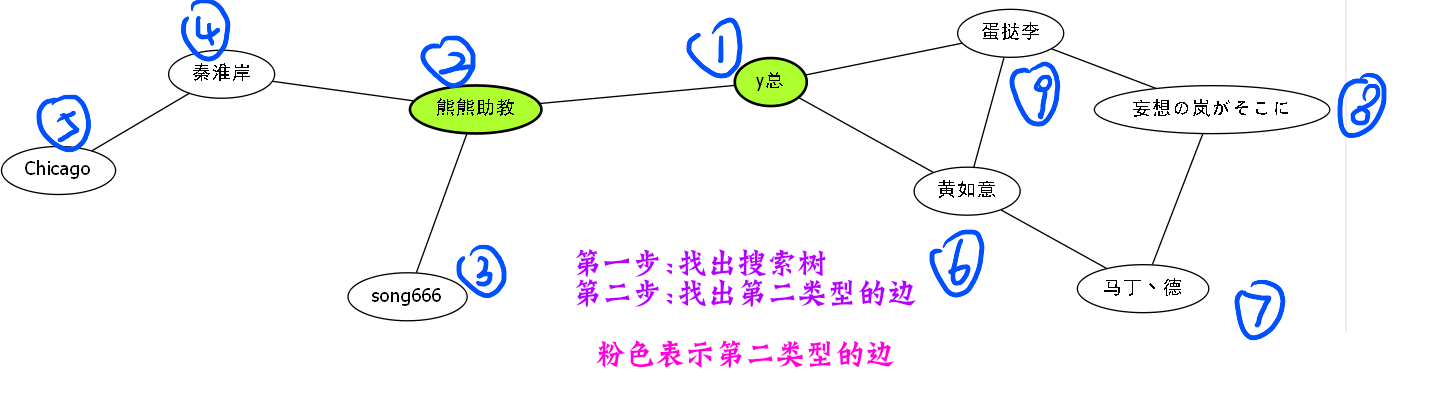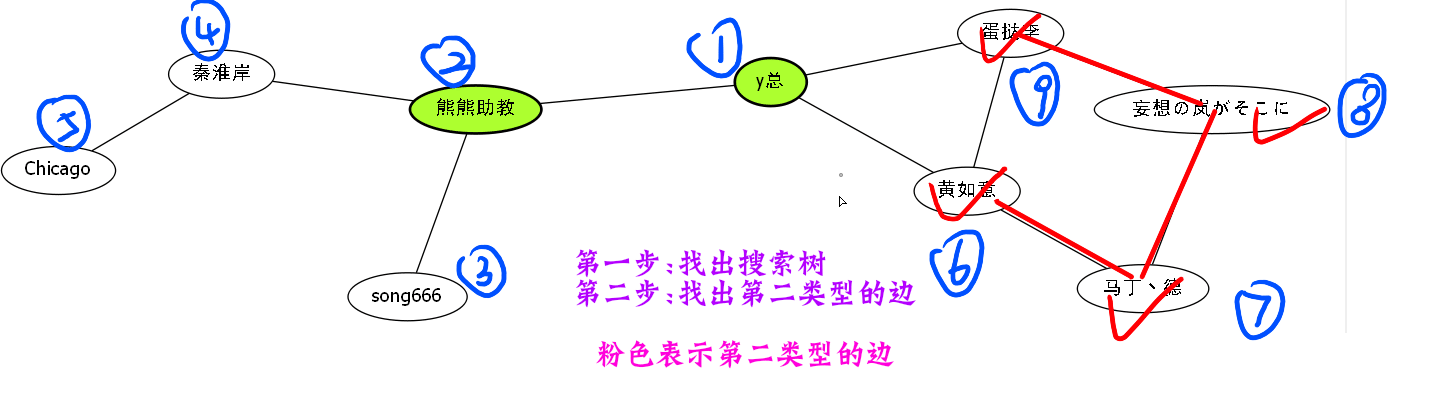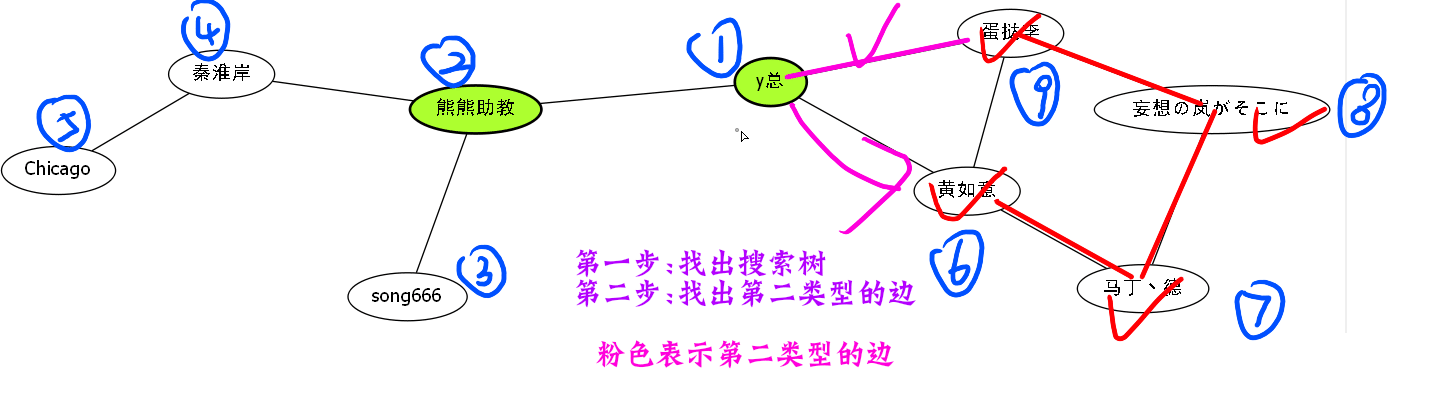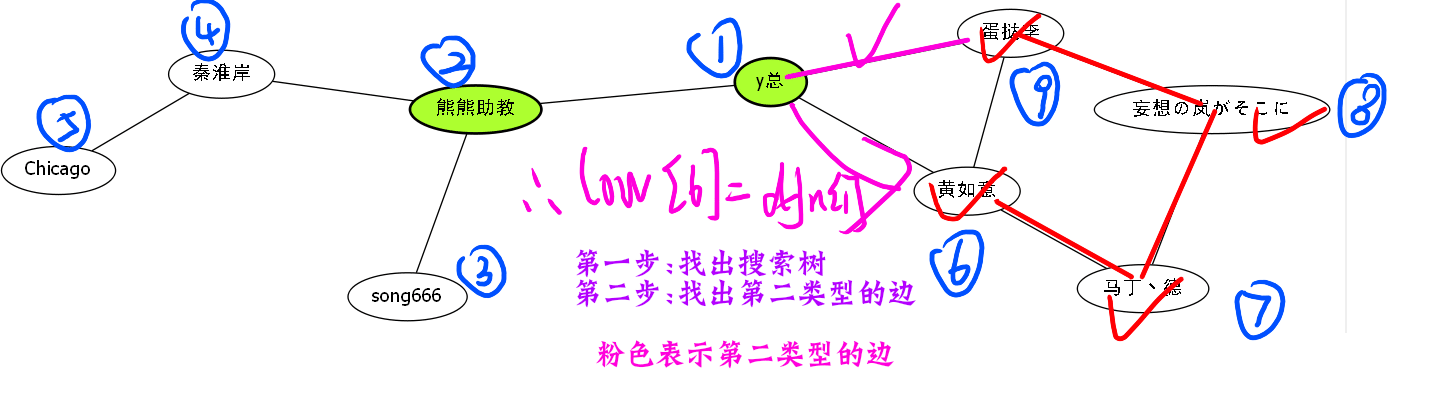
暂无,明天补充.今天的gif太累了.

Tarjan无向图的割点和桥(割边)详解&算法笔记&通俗易懂

原文：https://www.cnblogs.com/gzh-red/p/11253230.html